前言
典例剖析
解析:选 \(B\) . 理由如下:
由 \(f(x)+f(-x)+2x^2=0\) ,得到 \(f(x)+x^2=-f(-x)-(-x)^2\),令\(h(x)=f(x)+x^2\),则 \(h(x)=-h(-x)\),故 \(h(x)\) 为奇函数,
令 \(F(x)=f(x)+x^2-x\)此处涉及到构造函数的相关问题,如有兴趣,可参阅如下博文:
破解构造函数问题;
构造函数习题1;
构造函数习题2;
构造函数的难点和层次;
构造函数中的切入点;
再议构造函数;,则 \(F(x)=h(x)-x\),则\(F(x)\)为奇函数\(y\)\(=\)\(h(x)\)为奇函数,\(y\)\(=\)\(-x\)为奇函数,奇+奇=奇,是奇函数的一种比较常用的给出方式;,
由题目可知, 当\(x>0\) 时,\(F'(x)\)\(=\)\([f(x)+x^2-x]'\)\(=\)\(f'(x)\)\(+\)\(2x\)\(-1\)\(<0\)恒成立其目的是为了给出所构造的新函数的构造方向和将来构造的新函数的部分单调性,即函数 \(F(x)\) 在区间 \((0,+\infty)\)上单调递减,
又由于函数\(f(x)\)在 \(R\) 上存在导数为 \(f'(x)\)函数\(f(x)\)在 \(R\) 上可导,则函数 \(f(x)\) 必然在 \(R\) 上连续,从而导致 \(F(x)\) 在 \(R\) 上可导且连续,从而由 \(F(x)\) 在 \((0,+\infty)\) 上单调递减,可得到 \(F(x)\)必然会经过 \((0,0)\) 点,则会推知 \(F(x)\) 在 \([0,+\infty)\) 上单调递减,再结合其奇偶性就能知道在 \(R\) 上的单调性;,则函数\(f(x)\)在 \(R\) 上可导,则\(f(x)\)在 \(R\) 上连续,函数 \(F(x)\)在 \(R\) 上可导且连续,则函数 \(F(x)\) 在区间 \([0,+\infty)\)上单调递减,
又由于 函数 \(F(x)\) 为奇函数,则 在区间 \((-\infty,+\infty)\)上单调递减,
由 \(f(m)\geqslant f(1)-m^2+m\) 可得到, \(f(m)+m^2-m\geqslant f(1)\),即 \(f(m)+m^2-m\geqslant f(1)+1^2-1\),
即 \(F(m)\geqslant F(1)\),由于 \(F(x)\) 在 \(R\) 上单调递减,则可得到 \(m\leqslant 1\),则 \(m_{_{max}}=1\),故 选 \(B\) .
【解后反思】
①题目中给定对于任意实数 \(x\),都有 \(f(x)\)\(+\)\(f(-x)\)\(+\)\(2x^2\)\(=\)\(0\),是为了让我们构造函数 \(h(x)=f(x)+x^2\) 为奇函数;
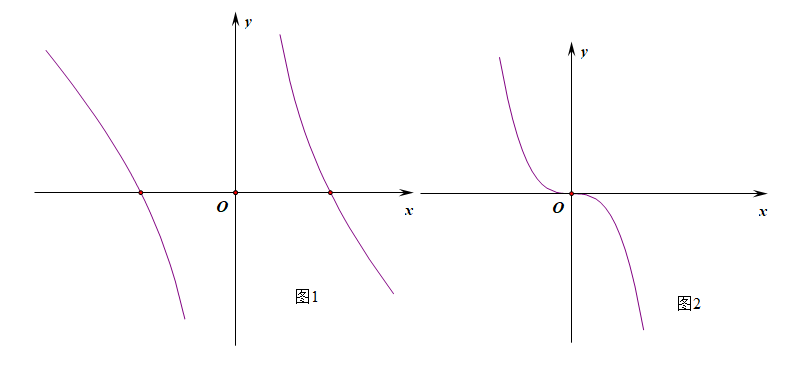
②题目中给定[当\(x>0\) 时,\(f'(x)+2x<1\)],能得到构造的函数 \(F(x)\) 在区间 \((0,+\infty)\) 上单调递减[如图\(1\)所示,虽然定义在 \(R\) 上,但是在 \(R\) 上并不单调],并不能得到在区间 \([0,+\infty)\) 上单调递减,再结合条件[在函数\(f(x)\)在 \(R\) 上存在导数为 \(f'(x)\)],则可以得到在区间 \([0,+\infty)\) 上单调递减[如图\(2\)所示],再结合奇函数则可以得到在 \((-\infty,+\infty)\) 上单调递减;
③函数在 \(R\) 上可导,则函数的图像在 \(R\) 上一定是连续的。