一.两个特殊的二叉树:
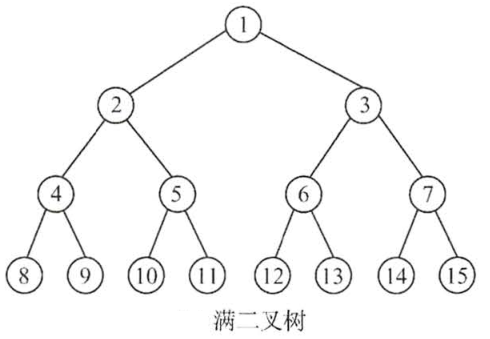
【1】满二叉树
一棵高度为h,且含有2^h-1个节点的二叉树成为'满二叉树',每层都含有最多节点,
满二叉树的叶子结点都集中在二叉树的最下一层,并且除叶子结点之外的'每个节点度数均为2'
满二叉树
【2】完全二叉树
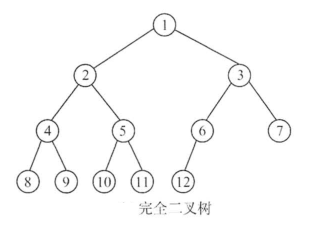
高度为h,有n个节点的二叉树,当且仅当每个节点都与高度为h的满二叉树编号为1~n的节点一一对应时
,称为'完全二叉树'
完全二叉树
特点:
[1]
若i<向下取整[n/2],则节点i为分支节点,否则为叶子节点
[2]
叶子节点只可能在层次最大的两层上出现,对于最大层次中的叶子结点,都依次排列在该层的最左边的位置上
[3]
若有度为1的节点,则只可能有一个,且该节点只有左孩子而无右孩子
[4]
若n为'奇数',则每个分支节点'都有左孩子和右孩子'
若n为'偶数',则编号最大的分支节点(编号为n/2)'只有左孩子,没有右孩子',
其余分支节点左右孩子都有。
【3】二叉排序树
'左子树'上的所有节点的关键字均小于根节点的关键字
'右子树'上的所有节点的关键字均大于根节点的关键字,
左右子树又各是一科二叉排序树
【4】平衡二叉树
树上任一节点的左子树和右子树的深度差'不超过1'
二.二叉树的性质
/1
非空二叉树上的叶子结点等于'度为2的节点'数加一,即N0=N2+1
/2
非空二叉树上的第K层上至多有2^(k-1)个节点
/3
高度为h的二叉树至多有(2^h)-1个节点
/4
具有n个结点的完全二叉树的高度为向上取整[log2(n+1)] (注:是以2为底的对数)
三.二叉树的存储结构
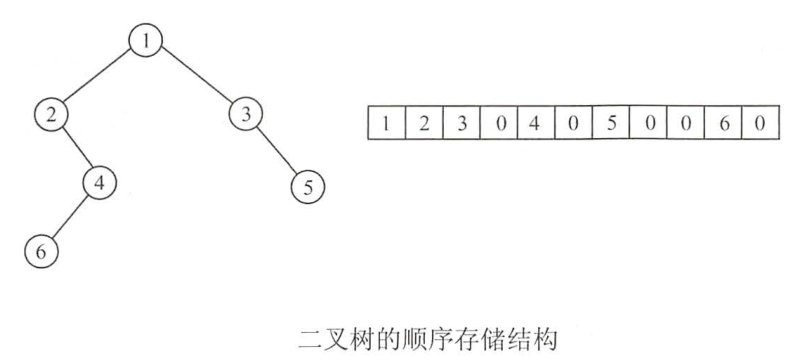
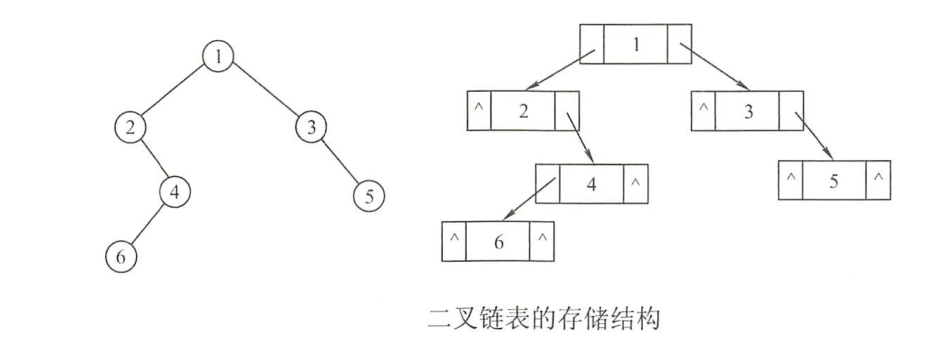
四.二叉树找两个节点的公共祖先
ElemType CommAncerster(SqTree T,int i,int j){
if(T[i]!='#' && T[j]!='#'){ //存在
while(i != j){
if(i > j){
i = i/2; //向上找i的祖先
}else{
j = j/2; //向上找j的祖先
}
}
return T[i];
}
}
五.二叉树的遍历
先序遍历
//根-->左-->右
void PreOrder(BiTree T){
if(T != NULL){
visit(T); //访问根节点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
}
中序遍历
//左-->根-->右
void InOrder(BiTree T){
if(T != NULL){
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根节点
InOrder(T->rchild); //递归遍历右子树
}
}
后序遍历
//左-->右-->根
void PostOrder(BiTree T){
if(T != NULL){
PostOrder(T->lchild); //递归遍历左子树
PostOrder(T->rchild); //递归遍历右子树
visit(T); //访问根节点
}
}
中序非递归代码
void InOrder2(BiTree T){
InitStack(S);
BiTree p = T; //p遍历指针
while(p || IsEmpty(S)){
if(p){
push(S,p); //当前节点入栈
p = p->lchild; //一直往左走
}else{
pop(S,p); //出栈并转向出栈节点的右子树
visit(p); //访问出栈节点
p = p->rchild; //一直往右走
}
}
}
先序非递归代码
void PreOrder(BiTree T){
InitStack(S);
BiTree p = T; //p遍历指针
while(p || IsEmpty(S)){
if(p){
visit(p); //访问当前结点
push(S,p); //当前节点入栈
p = p->lchild; //一直往左走
}else{
pop(S,p); //出栈并转向出栈节点的右子树
p = p->rchild; //一直往右走
}
}
}
层序遍历
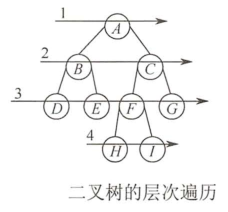
void LevelOrder(BiTree){
InitQueue(Q); //初始化的辅助队列
BiTree p;
EnQueue(Q,T); //根节点入队
while(!Empty(Q)){
DeQueue(Q,p); //队头出队
visit(p); //访问队头
if(p->lchild != NULL){ //左不空则入队
EnQueue(Q,p->lchild);
}if(p->rchild != NULL){ //右不空则入队
EnQueue(Q,p->rchild);
}
}
}
先序非递归代码
void PostOrder(BiTree T){
InitStack(S);
p = T;
r = NULL;
while(p || IsEmpty(S)){
if(p){ //走最左边
push(S,p);
p = p->lchild;
}else{ //向右
GetTop(S,p); //读栈顶节点(非出栈)
if(p->rchild && p->rchild!=r){ //若右子树存在,且未被访问过
p = p->rchild; //转向右
push(S,p); //压入栈
p = p->lchild; //再走到最左
}else{
pop(S,p); //否则弹出节点并访问
visti(p->data); //将节点弹出
r = p; //记录最近访问过的节点
p = NULL; //节点访问完后,重置p指针
}
}
}
}
六.线索二叉树
规定:若'无左子树',令'lchild'指向其'前驱结点';若'无右子树',令'rchild'指向其'后继节点'
示意图

中序遍历对二叉树线索化的递归算法
void InThreadTree(ThreadTree &p,ThreadTree &pre){
if(p != NULL){
//递归,线索化左子树
InThreadTree(p->lchild,pre);
if(p->lchild == NULL){ //左子树为空,建立前驱线索
p->lchild = pre;
p->ltag = 1;
}
if(pre!==NULL && pre->rchild==NULL){
pre->rchild = p; //建立前驱结点的后继线索
pre->rtag = 1;
}
pre = p;
InThreadTree(p->rchild,pre); //递归,线索化右子树
}
}
中序遍历
void CreateThread(ThreadTree T){
ThreadTree pre = NULL;
if(T != NULL){ //非空二叉树,线索化
InThread(T,pre);
pre->rchild = NULL; //处理遍历的最后一个节点
pre->rtag = 1;
}
}
示意图
