求方差的几个层次

前言

高考对方差的考察方式，也分几个层次。如下所述：

层次梳理

• 层次一：利用公式计算方差；

• 一组数据的方差计算公式：\(x_1，x_2，\cdots，x_{n}\)的平均数为\(\bar{x}=\cfrac{x_1+x_2+\cdots+x_{n}}{n}\)；

其方差为\(s^2=\cfrac{1}{n}[(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_{n}-\bar{x})^2]\)；

给定一组样本数据\(2，2，4，4，4\)，求这组数据的方差。

解析：先求平均数为 \(\bar{x} =\cfrac{2+2+4+4+4}{5}=3.2\)；

则方差为\(s^2=\cfrac{1}{5}[(2-3.2)^2\times 2+(4-3.2)^2\times 3]=(2-3.2)^2\times \cfrac{2}{5}+(4-3.2)^2\times \cfrac{3}{5}\)；

• 利用频率分布表计算方差；

【2019全国卷Ⅱ文科】某行业主管部门为了解本行业中小企业的生产情况，随机调查了 \(100\) 个企业， 得到这些企业第一季度相对于前一年第一季度产值增长率 \(y\) 的频率分布表.

(1)分别估计这类企业中产值增长率不低于\(40\%\) 的企业比例、产值负增长的企业比例；

解: 根据产值增长率频率分布表得， 所调查的 \(100\) 个企业中产值增长率不低于 \(40\%\) 的企业频率为 \(\cfrac{14+7}{100}=0.21\)， 产值负增长的企业频率为 \(\cfrac{2}{100}=0.02\)，用样本频率分布估计总体分布， 得这类企业中产值增长率不低于 \(40\%\) 的企业比例为 \(21\%\)， 产值负增长的企业比例为 \(2\%\).

(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表). ( 精确到 \(0.01\)，附: \(\sqrt{74}\approx 8.602\) )

解析： \(\bar{y}=\cfrac{1}{100}\times(-0.10\times 2+0.10\times 24+0.30\times 53+0.50\times 14+0.70 \times 7)=0.30\)，

\(s^{2}=\cfrac{1}{100}\times\)\([(-0.10-0.30)^{2}\times 2\)\(+\)\((0.10-0.30)^{2}\times 24\)\(+\)\((0.30-0.30)^{2}\times 53\)\(+\)\((0.50-0.30)^{2}\times 14\)\(+\)\((0.70-0.30)^{2}\times 7]\)

\(s^{2}=\cfrac{1}{100} \times\left[(-0.40)^{2} \times 2+(-0.20)^{2} \times 24+0^{2} \times 53+0.20^{2} \times 14+0.40^{2} \times 7\right]\)\(=0.0296\)，

\(s=\sqrt{0.0296}=0.02\times \sqrt{74} \approx 0.17 .\)

所以这类企业产值增长率的平均数与标准差的估计值分别为 \(0.30,0.17\).

• 随机变量的方差计算公式，如随机变量 \(X\) 服从贝努力分布\(X\sim B(n,p)\)，则方差 \(DX=np(1-p)\) .

【2017全国卷2理科13题高考真题】一批产品的二等品率为 \(0.02\) ，从这批产品中每次随机取一件，有放回的抽取 \(100\) 次， \(X\) 表示抽到的二等品件数，则 \(DX\) =________。

分析：本题目由于是有放回的抽取了 \(100\) 次，故应该相当于做了 \(100\) 次独立重复实验，故抽到的二等品件数应该服从二项分布，即\(X\sim B\left(100，0.02\right)\)

那么由随机变量的期望和方差公式可知\(n=100，p=0.02\)，\(EX=np=100\times 0.02=2\)，\(DX=np(1-p)=100\times0.02\times(1-0.02)=1.96\)。

• 层次二：利用性质计算方差；

• 平均数、方差、标准差的性质推广

如果一组样本数据\(x_1\)，\(x_2\)，\(\cdots\)，\(x_n\)，其平均数为\(\bar{x}\)，方差为\(s^2\)，标准差为\(s\)，

则样本数据\(ax_1+b\)，\(ax_2+b\)，\(\cdots\)，\(ax_n+b\)，其平均数为\(a\bar{x}+b\)，方差为\(a^2\cdot s^2\)，标准差为\(a\cdot s\)，

【2021年高三文数三轮模拟题】若样本 \(x_1+1\)， \(x_2+1\)， \(x_3+1\)， \(\cdots\)， \(x_n+1\) 的平均数为 \(10\)，方差为 \(2\)，则对于样本 \(2x_1+3\)， \(2x_2+3\)， \(2x_3+3\)， \(\cdots\)， \(2x_n+3\) ，下列结论正确的是【\(\quad\)】

$A.$平均数为 $20$，方差为 $4$

$B.$平均数为 $11$，方差为 $4$

$C.$平均数为 $21$，方差为 $8$

$D.$平均数为 $20$，方差为 $8$

解析：由于样本 \(x_1+1\)， \(x_2+1\)， \(x_3+1\)， \(\cdots\)， \(x_n+1\) 的平均数为 \(10\)，

则样本 \(x_1\)， \(x_2\)， \(x_3\)， \(\cdots\)， \(x_n\) 的平均数为 \(9\)，^[1]

对于样本 \(2x_1+3\)， \(2x_2+3\)， \(2x_3+3\)， \(\cdots\)， \(2x_n+3\)，

其平均数为 \(2\times 9+3=21\)，方差为 \(2^2\times 2=8\) ，故选 \(C\).

• 层次三：定性分析不计算，通过形[频率分布直方图]来判断方差的大小；

甲、乙、丙三位同学在一项集训中的 \(40\) 次测试分数都在 \([50,100]\) 内，将他们的测试分数分别绘制成频率分布直方图，如图所示，记甲、乙、丙的分数标准差分别为\(s_1\)，\(s_2\)，\(s_3\)，则它们的大小关系为【 】

$A.s_1 > s_2 > s_3$ $B.s_1 > s_3 > s_2$ $C.s_3 > s_1 > s_2$ $D.s_3 > s_2 > s_1$

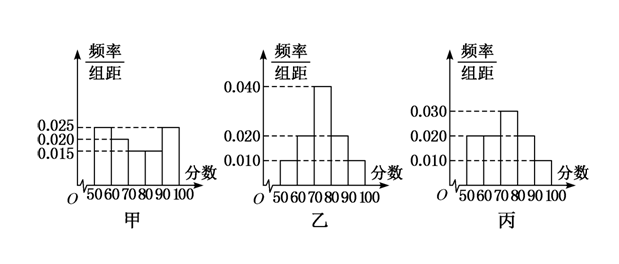
解析：根据给定的三个频率分布直方图知：第一组数据的两端数字较多，绝大部分数字都处在两端，数据偏离平均数远，最分散，其方差最大；第二组数据绝大部分数字都在平均数左右，数据最集中，其方差最小；第三组数据是单峰的每个小矩形的差别较小，数字分布均匀，数据没有第一组偏离平均数多，方差比第一组数据中的方差小，比第二组数据中的方差大．综上可得 \(s_1 > s_3 > s_2\)，故选 \(B\).

---

1. 解释：由于 \(\cfrac{(x_1+1)+(x_2+1)+\cdots+(x_n+1)}{n}=10\)，则 \(\cfrac{(x_1+x_2+\cdots+x_n)+n}{n}=10\)，
   即\(x_1+x_2+\cdots+x_n=9n\)，故 \(\cfrac{x_1+x_2+\cdots+x_n}{n}=9\)； ↩︎