前言
正弦定理
-
文字语言:在一个三角形中,各边和它所对角的正弦的比相等;
-
符号语言:(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
[拓展:(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC}=2R)((R)为三角形的外接圆的半径)];
定理证明
【思路一】:利用三角形的高证明正弦定理[易想易证];
证明:(1).设( riangle ABC)为锐角三角形时,设边(AB)上的高为(CD),根据锐角三角函数定义可知,
有(CD=acdot sinB);(CD=bcdot sinA);由此得到,(cfrac{a}{sinA}=cfrac{b}{sinB});
同理得到,(cfrac{b}{sinB}=cfrac{c}{sinC}),故(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC})在锐角三角形中成立;

(2).设( riangle ABC)为钝角三角形时,过点(C)做边(AB)上的高,交(AB)的延长线于点(D),根据锐角三角函数定义可知,
有(CD=acdot sinangle CBD=acdot sinangle ABC);(CD=bcdot sinA);由此得到,(cfrac{a}{sinA}=cfrac{b}{sinB});
同理得到,(cfrac{b}{sinB}=cfrac{c}{sinC}),故(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC})在钝角三角形中成立;
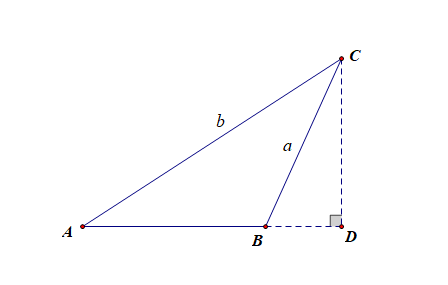
(3).当( riangle ABC)为直角三角形时,比如(C=cfrac{pi}{2}),容易验证(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC})成立;
综上所述,在( riangle ABC)中,一定有(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
【思路二】:利用三角形的面积证明正弦定理[易想易证];
证明:如图在( riangle ABC)中,边(AB)上的高为(CD),则(CD=acdot sinB),
则(S_{ riangle ABC}=cfrac{1}{2} imes AB imes CD=cfrac{1}{2}acsinB);

同理可得到(S_{ riangle ABC}=cfrac{1}{2}absinC=cfrac{1}{2}bcsinA);
则有(acsinB=absinC=bcsinA),同除以(abc),得到
(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
【思路三】:向量法证明正弦定理
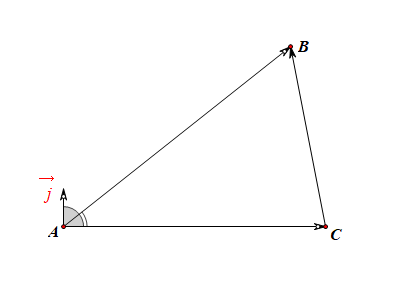
证明:(1).如图所示,设( riangle ABC)为锐角三角形,过点(A)做与(overrightarrow{AC})垂直的单位向量(vec{j}),
则由图可知,(<vec{j},overrightarrow{AC}>=90^{circ}),(<vec{j},overrightarrow{AB}>=90^{circ}-A),
(<vec{j},overrightarrow{CB}>=90^{circ}-C),延长两个向量可以看出来;且有(overrightarrow{AC}+overrightarrow{CB}=overrightarrow{AB}),
给上述的向量式同时取与向量(vec{j})的数量积,得到(vec{j}cdot (overrightarrow{AC}+overrightarrow{CB})=vec{j}cdotoverrightarrow{AB}),
整理得到,(vec{j}cdot overrightarrow{AC}+vec{j}cdotoverrightarrow{CB}=vec{j}cdotoverrightarrow{AB}),
则(|vec{j}||overrightarrow{AC}|cos90^{circ}+|vec{j}||overrightarrow{CB}|cos(90^{circ}-C)=|vec{j}||overrightarrow{AB}|cos(90^{circ}-A))
即(acdot sinC=ccdot sinA);即(cfrac{a}{sinA}=cfrac{c}{sinC});
过点(C)做与(overrightarrow{CB})垂直的单位向量(vec{i}),则由图可知,(<vec{i},overrightarrow{AC}>=90^{circ}-C),(<vec{i},overrightarrow{CB}>=90^{circ}),
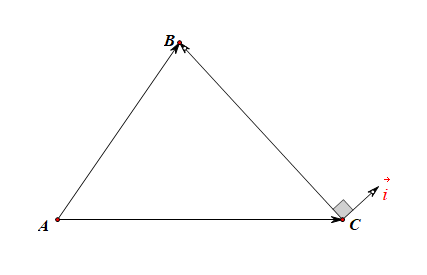
(<vec{i},overrightarrow{AB}>=90^{circ}-B),延长两个向量可以看出来;且有(overrightarrow{AC}+overrightarrow{CB}=overrightarrow{AB}),
给上述的向量式同时取与向量(vec{i})的数量积,得到(vec{i}cdot (overrightarrow{AC}+overrightarrow{CB})=vec{i}cdotoverrightarrow{AB}),
整理得到,(vec{i}cdot overrightarrow{AC}+vec{i}cdotoverrightarrow{CB}=vec{i}cdotoverrightarrow{AB}),
则(|vec{i}||overrightarrow{AC}|cos(90^{circ}-C)-+|vec{i}||overrightarrow{CB}|cos90^{circ}=|vec{i}||overrightarrow{AB}|cos(90^{circ}-B))
即(bcdot sinC=ccdot sinB);即(cfrac{b}{sinB}=cfrac{c}{sinC});
即( riangle ABC)为锐角三角形时,(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
(2).当( riangle ABC)为直角或者钝角三角形时,不妨令(Bgeqslant 90^{circ}),仿照上图放置角(B),
则同理可以证明(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
综上所述得到,(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});证毕。
【思路四】:三角形的外接圆证明
证明:(1).如图所示,设( riangle ABC)为锐角三角形,做出其外接圆(odot O),连结(BO)并延长交(odot O)于点(A'),
则由同弧所对的圆周角相等,得到(angle A=angle A'),
在(Rt riangle A'BC)中,(sinA'=cfrac{a}{2R}=sinA);
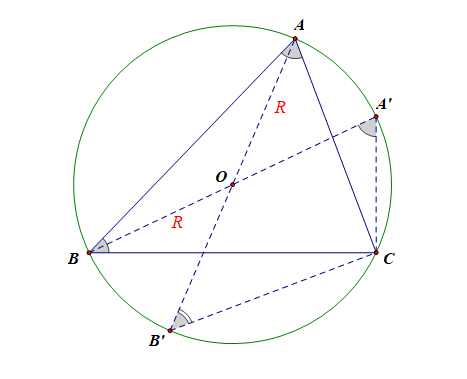
连结(AO)并延长交(odot O)于点(B'),则由同弧所对的圆周角相等,得到(angle B=angle B'),
在(Rt riangle AB'C)中,(sinB'=cfrac{b}{2R}=sinB);
同理得到,(cfrac{c}{2R}=sinC);故(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC}=2R);
(2).如图所示,若( riangle ABC)为直角三角形,做出其外接圆(odot O),连结(BO)并延长交(odot O)于点(A'),
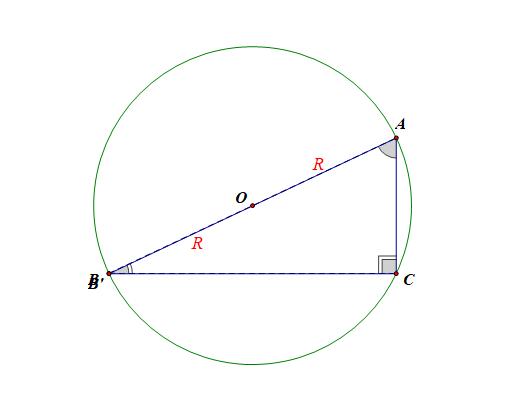
容易证明(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC}=2R);
(3).如图所示,若( riangle ABC)为钝角三角形,做出其外接圆(odot O),连结(BO)并延长交(odot O)于点(A'),
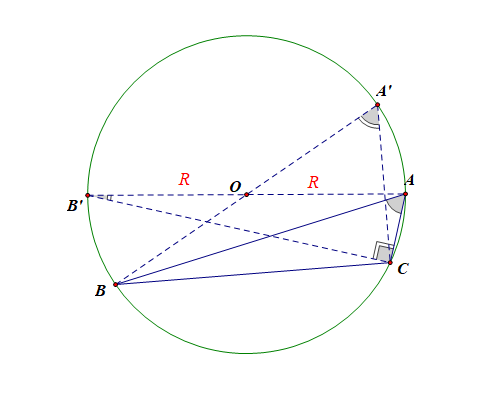
则由同弧所对的圆周角相等,得到(angle A=angle A'),在(Rt riangle A'BC)中,(sinA'=cfrac{a}{2R}=sinA);
连结(AO)并延长交(odot O)于点(B'),则由同弧所对的圆周角相等,得到(angle B=angle B'),
在(Rt riangle AB'C)中,(sinB'=cfrac{b}{2R}=sinB);
同理得到,(cfrac{c}{2R}=sinC);故(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC}=2R);
综上所述得到,(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
【思路五】:用余弦定理证明正弦定理
【思路六】:三角函数定义法
【思路七】:构造向量的射影法[教程上的证法]
如图所示,设( riangle ABC)为钝角三角形,以点(A)为原点,以射线(AB)的方向为(x)轴正方向建立直角坐标系,(C)点在(y)轴上的射影为(C'),
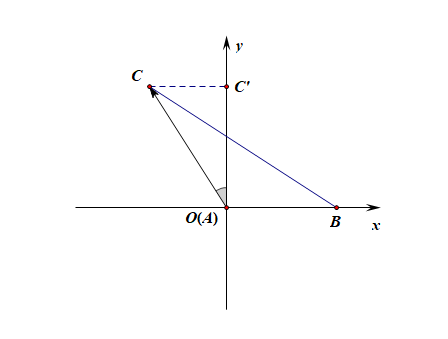
由于向量(overrightarrow{AC})与(overrightarrow{BC})在(y)轴上的射影均为(|overrightarrow{OC'}|),即
(|overrightarrow{OC'}|=|overrightarrow{AC}|cos(A-90^{circ})=bsinA),
又(|overrightarrow{OC'}|=|overrightarrow{BC}|sinB=asinB),
所以(asinB=bsinA),即(cfrac{a}{sinA}=cfrac{b}{sinB}),
同理,(cfrac{a}{sinA}=cfrac{c}{sinC}),
所以,(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});
若(A)为锐角或者直角,同理可得,(cfrac{a}{sinA}=cfrac{b}{sinB}=cfrac{c}{sinC});证毕。