福哥答案2021-02-11:
举例:"moonfudadayx"和"mfyudadxxax",最大公共子序列是"mfudadax",长度是8。
自然智慧即可。
1.递归。有代码。
三种情况。右移 右移;右移 不移;不移 右移。
2.动态规划。有代码。
dp[i][j]依赖左边,上边,左上边。
①.如果str1[i]==str2[j],dp[i][j]=【左上边】+1。
②.如果str1[i]!=str2[j],dp[i][j]=max(【左边】,【上边】)。
代码用golang编写,代码如下:
package main
import "fmt"
func main() {
str1 := "moonfudadayx"
str2 := "mfyudadxxax"
ret := longestCommonSubsequence1(str1, str2)
fmt.Println("递归:", ret)
ret = longestCommonSubsequence2(str1, str2)
fmt.Println("动态规划:", ret)
}
//递归
func longestCommonSubsequence1(s1 string, s2 string) int {
if len(s1) == 0 || len(s2) == 0 {
return 0
}
return process1(s1, s2, len(s1)-1, len(s2)-1)
}
func process1(str1 string, str2 string, i int, j int) int {
if i == 0 && j == 0 {
if str1[i] == str2[j] {
return 1
} else {
return 0
}
} else if i == 0 {
if str1[i] == str2[j] {
return 1
} else {
return process1(str1, str2, i, j-1)
}
} else if j == 0 {
if str1[i] == str2[j] {
return 1
} else {
return process1(str1, str2, i-1, j)
}
} else {
p1 := process1(str1, str2, i-1, j)
p2 := process1(str1, str2, i, j-1)
p3 := 0
if str1[i] == str2[j] {
p3 = 1 + process1(str1, str2, i-1, j-1)
}
return getMax(p1, getMax(p2, p3))
}
}
//动态规划
func longestCommonSubsequence2(str1 string, str2 string) int {
str1Len := len(str1)
str2Len := len(str2)
if str1Len > str1Len {
str1, str2 = str2, str1
str1Len, str2Len = str2Len, str1Len
}
if str1Len == 0 {
return 0
}
dp := make([][]int, str1Len)
for i := 0; i < str1Len; i++ {
dp[i] = make([]int, str2Len)
}
ret := 0
if str1[0] == str2[0] {
dp[0][0] = 1
}
for i := 1; i < str1Len; i++ {
if str1[i] == str2[0] {
dp[i][0] = 1
} else {
dp[i][0] = dp[i-1][0]
}
}
for j := 1; j < str2Len; j++ {
if str1[0] == str2[j] {
dp[0][j] = 1
} else {
dp[0][j] = dp[0][j-1]
}
}
for i := 1; i < str1Len; i++ {
for j := 1; j < str2Len; j++ {
if str1[i] == str2[j] {
dp[i][j] = 1 + dp[i-1][j-1]
} else {
dp[i][j] = getMax(dp[i-1][j], dp[i][j-1])
}
ret = getMax(ret, dp[i][j])
}
}
return ret
}
func getMax(a int, b int) int {
if a > b {
return a
} else {
return b
}
}
执行结果如下: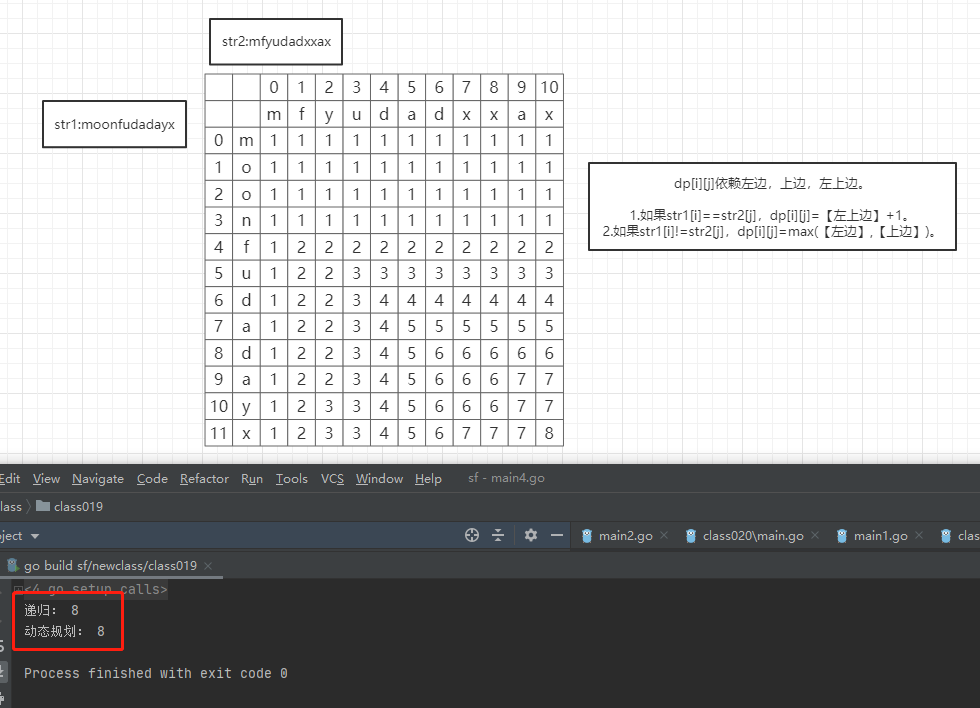
***
[左神java代码](https://github.com/algorithmzuo/algorithmbasic2020/blob/master/src/class19/Code04_LongestCommonSubsequence.java)
[评论](https://user.qzone.qq.com/3182319461/blog/1613023968)