本文首发于 vivo互联网技术 微信公众号
链接：https://mp.weixin.qq.com/s/2kea7-jACCJmSYBQAwXyIg
作者：刘洋
在 js 中进行数学的运算时，会出现0.1+0.2=0.300000000000000004的结果，一开始认为是浮点数的二进制存储导致的精度问题，但这似乎不能很好的解释为什么在同样的存储方式下0.3+0.4=0.7可以得到正确的结果。本文主要通过浮点数的二进制存储及运算，和IEEE754下的舍入规则，解释为何会出现这种情况。
一、浮点数的二进制存储
JavaScript遵循IEEE754标准，在64位中存储一个数据的有效数字形式。
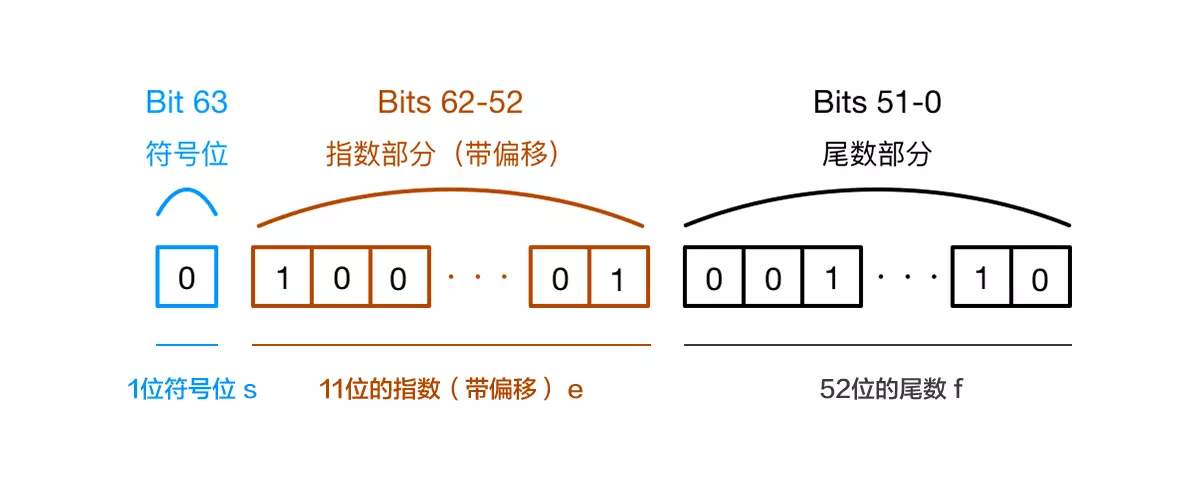
其中，第0位为符号位，0表示正数1表示负数；第1到11位存储指数部分；第12到63位存小数部分（尾数部分）（即有效数字）。由于二进制的有效数字总是表示为 1.xxx…的形式，尾数部分在规约形式下的第一位默认为1，故存储时第一位省略不写，尾数部分f存储有效数字小数点后的xxx...，最长52位。因此，JavaScript提供的有效数字最长为53个二进制位（尾数部分52位+被省略的1位）。
以0.1、0.2、0.3、0.4和0.7的二进制形式为例：
0.1->0.0001100110011...(0011无限循环)->0-01111111011-(1 .)1001100110011001100110011001100110011001100110011010(入)
0.2->0.001100110011...(0011无限循环)->0-01111111100-(1 .)1001100110011001100110011001100110011001100110011010(入)
0.3->0.01001100110011...(0011无限循环)->0-01111111101-(1 .)0011001100110011001100110011001100110011001100110011(舍)
0.4->0.01100110011...(0011无限循环)->0-01111111101-(1 .)1001100110011001100110011001100110011001100110011010(入)
0.7->0.101100110011...(0011无限循环)->0-01111111110-(1 .)0110011001100110011001100110011001100110011001100110(舍)
对于52位之后进行舍入运算，此时可看作0舍1入（具体舍入规则在第三部分详细说明），有精度损失。
二、对阶运算
由于指数位数不同，运算时需要进行对阶运算。对阶过程略，0.1+0.2与0.3+0.4的尾数求和结果分别如下：
0.1+0.2->10.0110011001100110011001100110011001100110011001100111
0.3+0.4->10.1100110011001100110011001100110011001100110011001101
求和结果需规格化（有效数字表示），右规导致低位丢失，此时需对丢失的低位进行舍入操作：
0.1+0.2->1.00110011001100110011001100110011001100110011001100111->1.0011001100110011001100110011001100110011001100110100(入)
0.3+0.4->1.01100110011001100110011001100110011001100110011001101->1.0110011001100110011001100110011001100110011001100110(舍)
即：
00111->0100
01101->0110
此处同样有精度损失。在这里我们可以发现，0.3+0.4对阶阶运算且规格化后的运算结果与0.7在二进制中的存储尾数相同（可对照尾数后几位），而0.1+0.2的运算结果与0.3的存储尾数不同，且0.1+0.2转化为十进制时结果为0.300000000000000004。
此时，虽然0.1+0.2与0.3+0.4进行舍入操作的近似位都为1，但一入一舍导致计算结果与“标准答案”的异同。
三、IEEE754标准下的舍入规则
维基百科对最近偶数舍入原则的解释如下：舍入到最接近，在一样接近的情况下偶数优先（Ties To Even，这是默认的舍入方式），即会将结果舍入为最接近（精度损失最小）且可以表示的值，但是当存在两个数一样接近的时候，则取其中的偶数（在二进制中是以0结尾的）。
首先要注意的是，保留小数不是只看后面一位或者两位，而是看保留位后面的所有位。
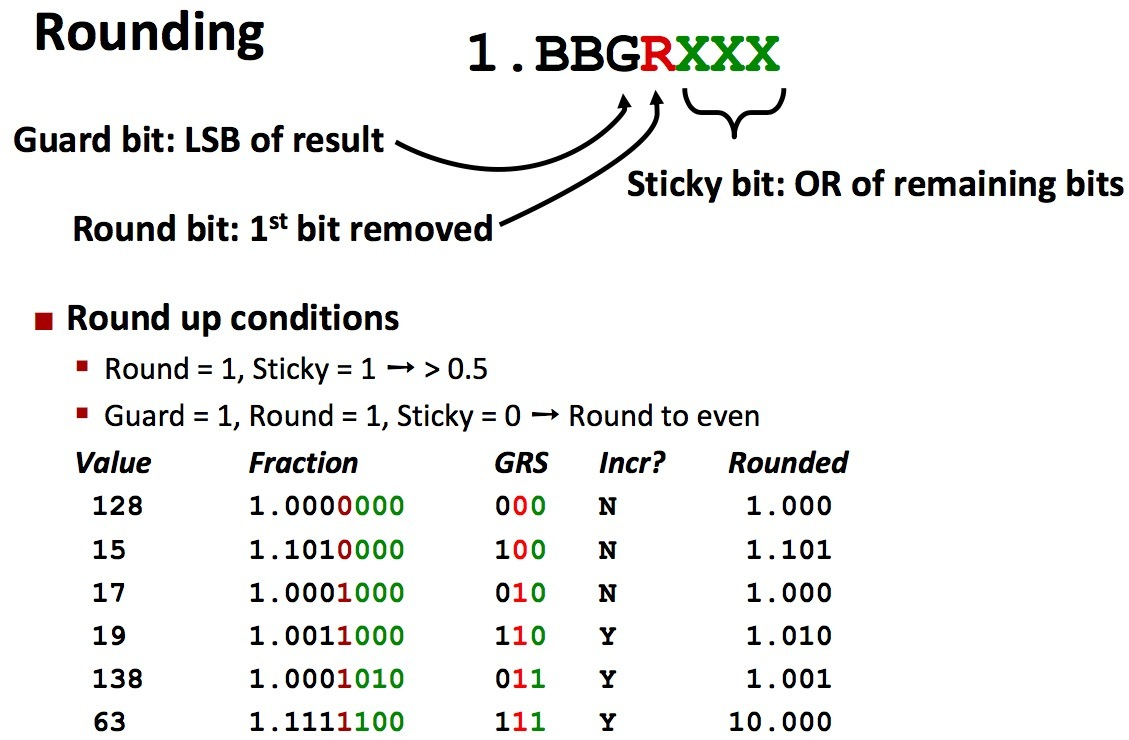
如图，可以看到近似需要看三位，保留位（近似后的最低位）、近似位（保留位的后一位）、粘滞位（sticky bit 近似位后的所有位进行或运算后看作一位）。
当粘滞位为1时，舍入规则可以看作0舍1入，近似位为0舍，近似位为1入（即第一部分小数二进制存储为52位尾数时所进行的舍入操作）。
当粘滞位为0时，若近似位为0则舍去。
当粘滞位为0时，若近似位为1，无论舍入精度损失都相同，故需取舍入两种结果中的偶数：保留位为1时入，保留位为0时舍（即第二部分对阶运算规格化时的舍入操作）。
四、总结思考
由于IEEE754标准，这样的“bug”不止在JavaScript中会出现，在所有采用该标准的语言中都会存在，实际编程中可以通过设置精度保留位数等方式解决。
更多内容敬请关注 vivo 互联网技术 微信公众号
注：转载文章请先与微信号：labs2020 联系。