Description
老C是个程序员。
作为一个懒惰的程序员,老C经常在电脑上玩方块游戏消磨时间。游戏被限定在一个由小方格排成的R行C列网格上,如果两个小方格有公共的边,就称它们是相邻的,而且有些相邻的小方格之间的公共边比较特殊。特殊的公共边排列得有很强的规律。首先规定,第1行的前两个小方格之间的边是特殊边。然后,特殊边在水平方向上每4个小方格为一个周期,在竖直方向上每2个小方格为一个周期。所有的奇数列与下一列之间都有特殊边,且所在行的编号从左到右奇偶交替。
下图所示是一个R=C=8的网格,蓝色标注的边是特殊边。首先,在第1行,第1列和第2列之间有一条特殊边。因为竖直方向周期为2,所以所有的奇数行,第1列和第2列之间都有特殊边。因为水平方向周期为4,所以所有奇数行的第5列和第6列之间也有特殊边,如果网格足够大,所有奇数行的第9列和第10列、第13列和第14列之间都有特殊边。因为所有的奇数列和下一列之间都有特殊边,所以第3列和第4列、第7列和第8列之间也有特殊边,而所在行的编号从左到右奇偶交替,所以它们的特殊边在偶数行。如果网格的规模更大,我们可以用同样的方法找出所有的特殊边。
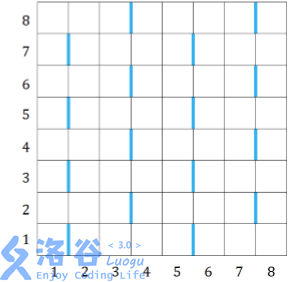
网格的每个小方格刚好可以放入一个小方块,在游戏的一开始,有些小方格已经放上了小方块,另外的小方格没有放。老C很讨厌下图所示的图形,如果他发现有一些小方块排列成了它讨厌的形状(特殊边的位置也要如图中所示),就很容易弃疗,即使是经过任意次旋转、翻转后排列成讨厌的形状,老C也同样容易弃疗。
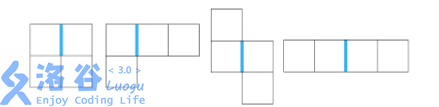
为了防止弃疗,老C决定趁自己还没有弃疗,赶紧移除一些格子里小方块,使得剩下的小方块不能构成它讨厌的形状。但是游戏里每移除一个方块都是要花费一些金币的,每个方块需要花费的金币有多有少参差不齐。老C当然希望尽可能少的使用游戏里的金币,但是最少要花费多少金币呢?老C懒得思考,就把这个问题交给你了。
Input
第一行有3个正整数C, R, n,表示C列R行的网格中,有n个小方格放了小方块。
接下来n行,每行3个正整数x, y, w,表示在第x列第y行的小方格里放了小方块,移除它需要花费w个金币。保证不会
重复,且都在网格范围内。
1 ≤ C, R, n ≤ 10^5 , 1 ≤ w ≤ 10^4
Output
输出一行,包含一个整数,表示最少花费的金币数量。
Sample Input
2 2 4
1 1 5
1 2 6
2 1 7
2 2 8
3 3 7
1 1 10
1 2 15
1 3 10
2 1 10
2 2 10
2 3 10
3 1 10
Sample Output
5
15
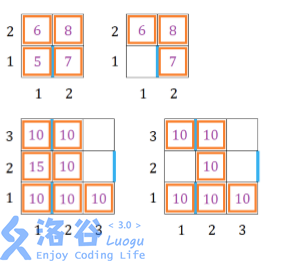
如图所示。
容易发现,如果不移除第1列第2行的
小方块,则至少要移除两个小方块,才能不包含老 C 讨厌的图形,花费至少20个金币;而删除第1列第2行 的小方块后,原有的讨厌图形全都不存在了,只需要 花费15个金币。
Solution
所以说还是开始写这个题的题解,洛谷A掉,BZOJWA了,但是笔者拍了1000+组数据并没有找到任何错误。。。。
网络流题目显然,不过貌似数据范围不大友好。。这时候就要相信信仰。
可以发现这个题目和行和列没有什么很大的关系,自然想到把放入小方块的格子当做点,那么连边就是一个问题了。
仔细看看给出的那四种图形,随便手玩一下就可以知道,这就是要求我们特殊线两边的格子除了互相之外不能连其他任何一个格子。否则就需要爆破。
那么这又有什么特殊的呢?经过再仔细观察我们可以发现,如果把这个图进行黑白染色,可以看出特殊线两边那两个格子一定是黑白两色,所以它们所连的格子也就是黑白两色的,这个时候就基本上确定这题要黑白染色求最小割了。
那么我们具体应该怎么搞掉这些方块呢?
不难发现的是,对于每一个特殊线两边的格子我们可能有的操作有三种:
1.与之相连的黑色方块全部爆破掉。
2.与之相连的白色方块全部爆破掉。
3.把这两个其中之一爆破掉。
我们根据黑白染色的情况放在左右边,先与S或者T连一条流量为自身花费的边,再与左或右端点连一条流量为无穷的边
嗯,这就差不多了,代码细节很多,希望自己考虑。
Code
// luogu-judger-enable-o2
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <set>
#include <map>
#define re register
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define get(a,b) ((a-1)*C+b)
#define col(a,b) ((a+b)%2)
#define MAXN 100005
#define MAXM 600005
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
map<ll,int> b;
map<ll,int> cost;
struct po
{
int nxt,to,w;
}edge[MAXM];
struct point
{
int x,y,w;
}a[MAXN];
int head[MAXN],dep[MAXN],num=-1;
int n,s,t,cur[MAXN],m;
int R,C;
inline int read()
{
int x=0,c=1;
char ch=' ';
while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
while(ch=='-')c*=-1,ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
return x*c;
}
inline void add_edge(int from,int to,int w)
{
edge[++num].nxt=head[from];
edge[num].to=to;
edge[num].w=w;
head[from]=num;
}
inline void add(int from,int to,int w)
{
add_edge(from,to,w);
add_edge(to,from,0);
}
inline bool bfs()
{
memset(dep,0,sizeof(dep));
queue<int> q;
while(!q.empty())
q.pop();
q.push(s);
dep[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(re int i=head[u];i!=-1;i=edge[i].nxt)
{
int v=edge[i].to;
if(dep[v]==0&&edge[i].w>0)
{
dep[v]=dep[u]+1;
if(v==t)
return 1;
q.push(v);
}
}
}
return 0;
}
inline int dfs(int u,int dis)
{
if(u==t)
return dis;
int diss=0;
for(re int& i=cur[u];i!=-1;i=edge[i].nxt)
{
int v=edge[i].to;
if(edge[i].w!=0&&dep[v]==dep[u]+1)
{
int check=dfs(v,min(dis,edge[i].w));
if(check!=0)
{
dis-=check;
diss+=check;
edge[i].w-=check;
edge[i^1].w+=check;
if(dis==0) break;
}
}
}
return diss;
}
inline int dinic()
{
int ans=0;
while(bfs())
{
for(re int i=0;i<=t;i++)
cur[i]=head[i];
while(int d=dfs(s,inf))
ans+=d;
}
return ans;
}
inline bool check(int p,int q)
{
if(p>=1&&p<=R&&q>=1&&q<=C) return 1;
else return 0;
}
int main()
{
freopen("date.in","r",stdin);
freopen("my.out","w",stdout);
memset(head,-1,sizeof(head));
C=read();R=read();n=read();
for(re int i=1;i<=n;i++){
a[i].y=read(),a[i].x=read(),cost[get(a[i].x,a[i].y)]=read();
b[get(a[i].x,a[i].y)]=i;
}
s=0,t=n+1;
for(re int i=1;i<=n;i++){
if(col(a[i].x,a[i].y)==0){
if(a[i].x%2==1){
if(a[i].y%4==1){
if(b[get(a[i].x,a[i].y-1)]&&check(a[i].x,a[i].y-1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y-1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}else if(a[i].y%4==2){
if(b[get(a[i].x,a[i].y+1)]&&check(a[i].x,a[i].y+1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y+1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}else if(a[i].y%4==3){
if(b[get(a[i].x,a[i].y-1)]&&check(a[i].x,a[i].y-1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y-1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}else {
if(b[get(a[i].x,a[i].y+1)]&&check(a[i].x,a[i].y+1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y+1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}
}else{
if(a[i].y%4==3){
if(b[get(a[i].x,a[i].y-1)]&&check(a[i].x,a[i].y-1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y-1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}else if(a[i].y%4==0){
if(b[get(a[i].x,a[i].y+1)]&&check(a[i].x,a[i].y+1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y+1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}else if(a[i].y%4==1){
if(b[get(a[i].x,a[i].y-1)]&&check(a[i].x,a[i].y-1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y-1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
} else {
if(b[get(a[i].x,a[i].y+1)]&&check(a[i].x,a[i].y+1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y+1)],inf);
if(b[get(a[i].x-1,a[i].y)]&&check(a[i].x-1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x-1,a[i].y)],inf);
if(b[get(a[i].x+1,a[i].y)]&&check(a[i].x+1,a[i].y)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x+1,a[i].y)],inf);
}
}
} else {
if(a[i].x%2==1){
if(a[i].y%4==1){
if(b[get(a[i].x,a[i].y+1)]&&check(a[i].x,a[i].y+1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y+1)],min(cost[get(a[i].x,a[i].y)],cost[get(a[i].x,a[i].y+1)]));
}
else if(a[i].y%4==2){
if(b[get(a[i].x,a[i].y-1)]&&check(a[i].x,a[i].y-1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y-1)],min(cost[get(a[i].x,a[i].y)],cost[get(a[i].x,a[i].y-1)]));
}
}else{
if(a[i].y%4==3){
if(b[get(a[i].x,a[i].y+1)]&&check(a[i].x,a[i].y+1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y+1)],min(cost[get(a[i].x,a[i].y)],cost[get(a[i].x,a[i].y+1)]));
}
else if(a[i].y%4==0){
if(b[get(a[i].x,a[i].y-1)]&&check(a[i].x,a[i].y-1)) add(b[get(a[i].x,a[i].y)],b[get(a[i].x,a[i].y-1)],min(cost[get(a[i].x,a[i].y)],cost[get(a[i].x,a[i].y-1)]));
}
}
}
}
for(re int i=1;i<=n;i++){
if(col(a[i].x,a[i].y)==1){
if(a[i].x%2==1){
if(a[i].y%4==1||a[i].y%4==2) continue;
add(b[get(a[i].x,a[i].y)],t,cost[get(a[i].x,a[i].y)]);
}else{
if(a[i].y%4==3||a[i].y%4==0) continue;
add(b[get(a[i].x,a[i].y)],t,cost[get(a[i].x,a[i].y)]);
}
}else{
if(a[i].x%2==1){
if(a[i].y%4==1||a[i].y%4==2) continue;
add(s,b[get(a[i].x,a[i].y)],cost[get(a[i].x,a[i].y)]);
}else{
if(a[i].y%4==3||a[i].y%4==0) continue;
add(s,b[get(a[i].x,a[i].y)],cost[get(a[i].x,a[i].y)]);
}
}
}
cout<<dinic();
return 0;
}