先说一下矩阵乘法的定义:
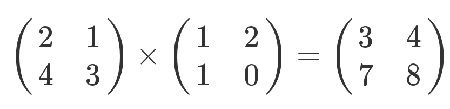
也就是说,结果矩阵第$m$行与第$n$列交叉位置的那个值,等于第一个矩阵第$m$行与第二个矩阵第$n$列,对应的位置的每个值的乘积之和。
公式则是:其中$C_{ij}$为A的第$i$行与B的第$j$列对应的乘积的和,即:
$Cij =Σaik*bkj(1<=i<=n,1<=j<=n,1<=k<=n)$。
矩阵乘法的代码:
const int N=100;
int c[N][N]; //c是最终的矩阵
void multi(int a[][N],int b[][N],int n)
{
memset(c,0,sizeof c);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
c[i][j]+=a[i][k]*b[k][j];
}
快速幂
求幂时我们常常会因结果太大而导致速度很慢,这时候我们就需要运用倍增的思想特殊的乘法应运而生————快速幂。
举个例子,如果$a_{10}$,我们需要求十次,而如果我们用了快速幂就可以把$a_{10}$转变为二进制的形式从而加快运算速度
引入一个定义*单位矩阵(对角线为1其余都为0,一个矩阵乘单位矩阵为它本身)
void qpow(long long k){
for(int i=1; i<=n; i++)
I.a[i][i]=1;
while(k>0) {
if(k%2==1) I=I*a;
a=a*a;
k=k>>1;
}
}
本题的完整代码:
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #define ll long long
6 #define maxn 105
7 #define mo 1000000007
8 using namespace std;
9 int n;
10 struct mul{
11 ll a[maxn][maxn];
12 }a,I;
13 mul operator *(const mul &x,const mul &y){ //重载运算符
14 mul z;
15 memset(z.a,0,sizeof(z.a));
16 for(int k=1;k<=n;k++)
17 for(int i=1;i<=n;i++)
18 for(int j=1;j<=n;j++)
19 z.a[i][j]=(z.a[i][j]+x.a[i][k]*y.a[k][j]%mo)%mo;
20 return z;
21 }
22 ll k;
23 inline void init(){
24 scanf ("%lld%lld",&n,&k);
25 for(int i=1;i<=n;++i)
26 for(int j=1;j<=n;++j)
27 scanf ("%lld",&a.a[i][j]);
28 }
29 void qpow(long long k){
30 for(int i=1; i<=n; i++)
31 I.a[i][i]=1;
32 while(k>0) {
33 if(k%2==1) I=I*a;
34 a=a*a;
35 k=k>>1;
36 }
37 }
38 int main(){
39 init();
40 qpow(k);
41 for(int i=1;i<=n;++i){
42 for(int j=1;j<=n;++j)
43 printf("%d ",I.a[i][j]);
44 cout<<endl;
45 }
46 return 0;
47 }
在斐波那契数列之中
$f[i] = 1*f[i-1]+1*f[i-2] f[i-1] = 1*f[i-1] + 0*f[i-2]$;
所以我们可以构建一个矩阵做幂运算后,可以得到我们需要的矩阵,求得的矩阵为:
1 1
1 0
所以这里我是直接求解n次幂,答案就是$a[0][1]$;
代码如下:
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #define ll long long
6 #define maxn 105
7 #define mo 1000000007
8 using namespace std;
9 struct mul{
10 ll a[maxn][maxn];
11 }a,I;
12 mul operator *(const mul &x,const mul &y){ //重载运算符
13 mul z;
14 memset(z.a,0,sizeof(z.a));
15 for(int k=1;k<=2;k++)
16 for(int i=1;i<=2;i++)
17 for(int j=1;j<=2;j++)
18 z.a[i][j]=(z.a[i][j]+x.a[i][k]*y.a[k][j]%mo)%mo;
19 return z;
20 }
21 ll k;
22 inline void init(){
23 scanf ("%lld",&k);
24 a.a[1][1]=a.a[1][2]=a.a[2][1]=1;
25 a.a[2][2]=0;
26 }
27 void qpow(long long k){
28 for(int i=1; i<=2; i++)
29 I.a[i][i]=1;
30 while(k>0) {
31 if(k%2==1) I=I*a;
32 a=a*a;
33 k=k>>1;
34 }
35 }
36 int main(){
37 init();
38 qpow(k);
39 cout<<I.a[1][2];
40 return 0;
41 }