汇思学 18国庆 数论

　　　　　　数论

1.快速幂

typedef long long LL;

LL qpow(int a, int b) {  //快速幂 
    LL res = 1;
    while (b) {
        if (b & 1) res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}

LL mul(int a, int b) {  //快速乘 
    LL res = 0;
    while (b) {
        if (b & 1) res = (res + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return res;
}

2.逆元
（1）费马小定理求逆元

　　若 p 是质数，且 p 不是 a 的约数

　　根据费马小定理有：a^{p - 1} ≡ 1 (mod p)

　　所以 a 的逆元 x = a^{p - 2}

（2）欧拉定理求逆元

　　若 a 与 p 互质

　　根据欧拉定理有：a^φ(p) = 1 (mod p)

　　所以 a 的逆元 x = a^{φ(p) - 1}

3.最大公约数 gcd
（1）从大到小枚举
（2）分解质因数求解
（3）更相减损术 gcd(a, b) = gcd(a - b, b)
（4）辗转相除法 gcd(a, b) = gca(a % b, b)

int gcd(int x, int y) {
    return y == 0 ? x : gcd(x, x % y);
}

4.最小公倍数 lcm

int lcm(int x, int y) {
    return x / gcd(x, y) * y;
}

5.扩展欧几里德 exgcd
（1）ax + by = gcd(a, b)
（2）X = x + b/gcd * k, Y = y - a/gcd * k;
（3）ax + by != k*gcd(a, b） （k != 0） 此时无解
（4）令k = c/gcd(a, b)
相当于求 k * (ax + by) = gcd(a, b) * k
求出ax + by = gcd(a, b)后，将解乘k即可

void ex_gcd(LL a, LL b, LL &d, LL &x, LL &y) {
    if (!b) { d = a; x = 1; y = 0; }
    else { ex_gcd(b, a % b, d, y, x); y -= x * (a / b); }
}

6.同余

　　a ≡ b (mod p) → (a - b) mod p = 0;

　　ax ≡ 1 (mod b) 相当于 ax + by = 1

　　当 a , b 互质时有解

　　用 exgcd 求出一组一组解，然后再求出最小正整数解

7.同余方程组
考虑方程组 x ≡ r1(mod m1)

　　　　　x ≡ r2(mod m2) 

　　x = k1 * m1 + r1 = k2 * m2 + r2 → k1 * m1 - k2 * m2 = r2 - r1

　　相当于 ax + by = c
8.离散对数
9.线性筛素数

for (int i = 2; i <= n; ++i) {
    if (!bz[i]) pri[++cnt] = i;
    for (int j = i; j <= cnt; ++j) {
        if (i * pri[j] > n) break;
        bz[i * pri[j]] = 1;
        if (i % pri[j] == 0) break;  //保证了每个数只会被筛一次
                //只会被自己最小的质因子筛掉
    }
}

10.欧拉函数
　　线性筛法求欧拉函数

//在筛素数时顺便求出欧拉函数
for (int i = 2; i <= n; ++i) {
    if (!bz[i]) pri[++cnt] = i, phi[i] = i - 1;
    for (int j = 1; j <= cnt; ++j) {
        if (i * pri[j] > n) break;
        bz[i * pri[j]] = 1;
        if (i % pri[j] != 0) phi[i * pri[j]] = phi[i] * (pri[j] - 1);
        if (i % pri[j] == 0) {
            phi[i * pri[j]] = phi[i] * pri[j];
            break;
        }
    }
}

11.组合数
（1）C(m, n) = m! / n!(m - n)!
例题：NOIP2016 D2T1 组合数问题
解：杨辉三角预处理，求二维前缀和 f[i][j] ，并在过程中对 k 取模，根据 f[i][j] 的值是否为 0 判断是否为 k 的倍数
（2）Lucas定理

（3）若数据范围不大（0 ≤ n ≤ m ≤ 10⁵, 1 ≤ p ≤ 10⁹），可直接预处理阶乘和阶乘的逆元，直接计算

（4）一些比较有用的公式

                

12.容斥原理

　　

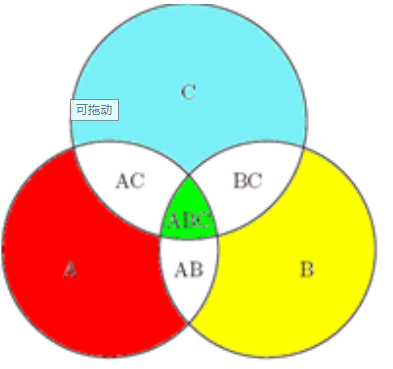
如图，总面积为 A + B + C - AC - AB - BC + ABC

容斥的重要功能就是化繁为简

13.斐波纳契数列

　　f[0] = f[1] = 1;

　　f[i] = f[i - 1] + f[i - 2];

14.卡特兰数

　　C(1) = 1;

　　C(n) = C(1) * C(n - 1) + C(2) * C(n - 2) + …+ C(n - 1) * C(1);

通项公式：C(n + 1) = C(2n, n) - C(2n, n - 1);

15.错排

考虑一个有 n 个元素的排列，若一个排列中所有的元素都不在自己原来的位置上，那么就称这样的一个排列为原排列的一个错排

n 个元素的错排记为 D(n)

　　D(1) = 0; D(2) = 1;

　　D(n) = (n - 1)(D(n - 1) + D(n - 2));

16.高斯消元

　　（1）用于解多元一次方程组

　　（2）异或高斯消元

　　　相当于把加减换成异或，其实更简单一些

17.概率与期望
　　独立事件之间的概率和期望可以分别相加求解

　　（1）贝叶斯公式
　　P(B|A) 表示事件A一定发生的情况下，事件B发生的概率
　　当事件A，B有关联时，P(AB) = P(B|A) * P(A)
　　反之 P(AB) = P(A) * P(B)
　　（2）期望的可乘性
　　（3）DP类的期望题
　　  DP方程一般设法：
　　　　f[i]表示 i 到终点的期望，按照i递减来推
　　　　f[i]表示起点到 i 点的期望，按照 i 递增来推
18.矩阵乘法
（1）运算公式

void mul() { //矩阵乘法
    for(int i = 1; i <= n; ++i)
        for(int k = 1; k <= m; ++k) {
            int r = a[i][k];
            for(int j = 1; j <= l; ++j)
                c[i][j] += r * b[k][j];
        }
    /*
    另一种写法 
　　若把三重循环中的i,j,k枚举顺序交换，速度可能慢几倍
    for(int i=1;i<=h;i++)
        for(int j=1;j<=l;j++)
            for(int k=1;k<=ll;k++)
                c[i][k] += a[i][j] * b[j][k];
    */
}

（2）矩阵快速幂加速

struct Mat {
    ll m[101][101];
} a, e;

Mat Mul(Mat x, Mat y) {
    Mat c;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            c.m[i][j] = 0;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            for (int k = 1; k <= n; ++k)
                c.m[i][j] = c.m[i][j] % mod + x.m[i][k] * y.m[k][j] % mod;
    return c;
}

Mat pow(Mat x, ll y) {
    Mat ans = e;
    while (y) {
        if (y & 1) ans = Mul(ans, x);
        x = Mul(x, x);
        y >>= 1;
    }
    return ans;
}

19.博弈论

 咕咕咕。。。

已完结。。。