题意:用一个字符串表示树,0代表向下走,1代表往回走,求两棵树是否同构。
分析:同构的树经过最小表示会转化成两个相等的串。
方法:递归寻找每一棵子树,将根节点相同的子树的字符串按字典序排列,递归回去即可。最终得到的串将是这棵树的最小表示。
举例:0010011101001011,表示的树如下
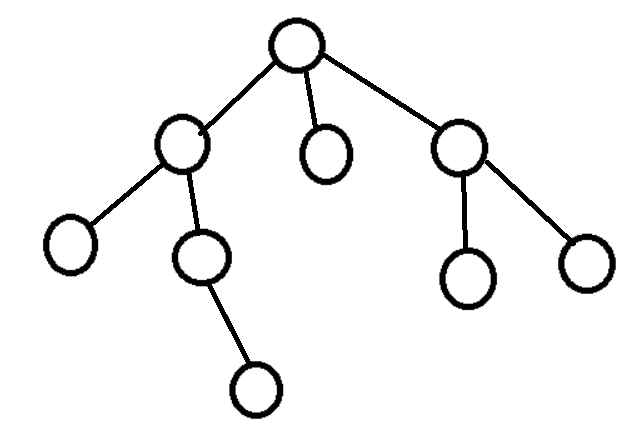
根节点下的三棵子树分别为00100111、01、001011
大的原则是:递归过程中,每次都将当前这棵树的所有子树的字符串排序。
00100111这棵子树,将它的根结点设为S,它的子树是01和0011,那么应该在S处将这两棵子树按字典序排列,结果是001101,而最终递归结束返回的结果是00011011(在001101的前面加了个0,后面加了个1),递归的作用是更新每一棵子树,使其按照最小字典序的字符串表示,这样处理,会使同构的树经过最小表示转化成两个相等的串。
#include<cstdio> #include<cstring> #include<cstdlib> #include<cctype> #include<cmath> #include<iostream> #include<sstream> #include<iterator> #include<algorithm> #include<string> #include<vector> #include<set> #include<map> #include<stack> #include<deque> #include<queue> #include<list> #define Min(a, b) a < b ? a : b #define Max(a, b) a < b ? b : a typedef long long ll; typedef unsigned long long llu; const int INT_INF = 0x3f3f3f3f; const int INT_M_INF = 0x7f7f7f7f; const ll LL_INF = 0x3f3f3f3f3f3f3f3f; const ll LL_M_INF = 0x7f7f7f7f7f7f7f7f; const int dr[] = {0, 0, -1, 1}; const int dc[] = {-1, 1, 0, 0}; const double pi = acos(-1.0); const double eps = 1e-8; const int MAXN = 3000 + 10; const int MAXT = 10000 + 10; using namespace std; char a[MAXN], b[MAXN]; string dfs(string s){ vector<string> v; int len = s.size(); int deep = 0, start = 0; for(int i = 0; i < len; ++i){ if(s[i] == '0') ++deep; else --deep; if(deep == 0){ string tmp = s.substr(start + 1, i - start - 1); if(tmp == ""){ v.push_back("01"); } else{ tmp = dfs(tmp); v.push_back("0" + tmp + "1"); } start = i + 1; } } sort(v.begin(), v.end()); string ans = ""; len = v.size(); for(int i = 0; i < len; ++i){ ans += v[i]; } return ans; } int main(){ int T; scanf("%d", &T); while(T--){ scanf("%s%s", a, b); string s1 = dfs(a); string s2 = dfs(b); if(s1 == s2) printf("same\n"); else printf("different\n"); } return 0; }