一、本文内容
最长递增子序列的两种动态规划算法实现,O(n^2)及O(nlogn).
二、问题描述
最长递增子序列:给定一个序列,从该序列找出最长的 升序/递增 子序列。
特点:1、子序列不要求连续; 2、子序列在原序列中按严格(strictly)升序排序; 3、最长递增子序列不唯一。
注:下文最长递增子序列用缩写LIS表示。
example:
0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
对应的LIS:
0, 2, 6, 9, 13, 15
0, 4, 6, 9, 11, 15
三、算法描述
1、考察第i+1个元素时,不考虑前面i个元素的状态
给定长度为n的序列A[0..n-1],对于给定某个的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能间接通过当前状态来影响;换句话说,每个状态都是过去历史的完整总结。即LIS[i]当前的状态与LIS[0..i-1]已无关。这几句话可以用Fibonacci的递归树来验证,对LIS的递归树同样适用。 如下面的递归树:
LIS(3)
/ |
LIS(2) LIS(1) LIS(0)
/ /
LIS(1) LIS(0) LIS(0)
/
LIS(0)
很显然,递归树有很多重复/重叠的子问题,而大问题的最优解又可以由这些子问题的最优解得到,符合DP的两个条件,故可以用DP来解决LIS问题。
那么给定序列A[0..n-1],求它的LIS,可以top-down分解任务,得到递归树;递归树bottom-up就可以建立子问题的查询表以供求解当前问题时查询。
这就是DP的两种处理方式:Memoization(top-down) 和 Tabulation (bottom-up).
假设LIS[i]表示A[0..i]的最长递增子序列的长度,那么
LIS[i+1] = max{1, LIS[j]+1}, A[i+1]>A[j], for any j<=i; 注意:到A[i]的子序列长度不一定大于A[j]的子序列长度(如上例当A[j]=12, LIS[j]={0, 4, 12}和当A[i]=2, LIS[i]={0, 2})
若A[i+1]>A[j],则A[i+1]可以接在LIS[j]长的子序列后面构成一个更长的子序列。
同时, 从A[i+1]开始又构成一个长度为1的子序列。故两者取大值。
2、考察第i+1个元素时,考虑前面i个元素的状态
那么,什么时候在一个已存在的序列中添加或者替换一个元素是安全的呢?(DP算法都是offline algorithm,需要全局考虑)
显然,我们需要维护所有递增的子序列(称其为active list,即可能成为max{LIS}的子序列)。而这些子序列的长度都不同,
可以按照插入排序的思想,一个一个元素地从前面找到其应该归属的子序列(active list)。
有A[i]>A[i-1]和A[i]<A[i-1]两种情况,A[i]<A[i-1]又有一种特殊情况A[i]是当前序列中的最小元素,即A[i]<A[j], for any j<i;
case 1. If A[i] is smallest among all end candidates of active lists, we will start new active list of length 1.
(when we encounter new smallest element in the array, it can be a potential candidate to start new sequence,{2, 5, 3, 1, 2, 3, 4, 5, 6})
case 2. If A[i] is largest among all end candidates of active lists, we will clone the largest active list, and extend it by A[i].
case 3. If A[i] is in between, we will find a list with largest end element that is smaller than A[i]. Clone and extend this list by A[i]. We will discard all other lists of same length as that of this modified list.
(找到end element小于A[i]的active list之后,其他相同长度的active list将被删除,因为A[i]小于这些等长active list的end element,用新的active list代替将被删除的active list:复制小于A[i]的active list,并添加A[i])
处理过程如下
example:A[ ] = {0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}
A[0] = 0. Case 1. There are no active lists, create one.
0.
-----------------------------------------------------------------------------
A[1] = 8. Case 2. Clone and extend.
0.
0, 8.
-----------------------------------------------------------------------------
A[2] = 4. Case 3. Clone, extend and discard.
0.
0, 4.
0, 8. Discarded
-----------------------------------------------------------------------------
A[3] = 12. Case 2. Clone and extend.
0.
0, 4.
0, 4, 12.
-----------------------------------------------------------------------------
A[4] = 2. Case 3. Clone, extend and discard.
0.
0, 2.
0, 4. Discarded.
0, 4, 12.
-----------------------------------------------------------------------------
A[5] = 10. Case 3. Clone, extend and discard.
0.
0, 2.
0, 2, 10.
0, 4, 12. Discarded.
-----------------------------------------------------------------------------
A[6] = 6. Case 3. Clone, extend and discard.
0.
0, 2.
0, 2, 6.
0, 2, 10. Discarded.
-----------------------------------------------------------------------------
A[7] = 14. Case 2. Clone and extend.
0.
0, 2.
0, 2, 6.
0, 2, 6, 14.
-----------------------------------------------------------------------------
A[8] = 1. Case 3. Clone, extend and discard.
0.
0, 1.
0, 2. Discarded.
0, 2, 6.
0, 2, 6, 14.
-----------------------------------------------------------------------------
A[9] = 9. Case 3. Clone, extend and discard.
0.
0, 1.
0, 2, 6.
0, 2, 6, 9.
0, 2, 6, 14. Discarded.
-----------------------------------------------------------------------------
A[10] = 5. Case 3. Clone, extend and discard.
0.
0, 1.
0, 1, 5.
0, 2, 6. Discarded.
0, 2, 6, 9.
-----------------------------------------------------------------------------
A[11] = 13. Case 2. Clone and extend.
0.
0, 1.
0, 1, 5.
0, 2, 6, 9.
0, 2, 6, 9, 13.
-----------------------------------------------------------------------------
A[12] = 3. Case 3. Clone, extend and discard.
0.
0, 1.
0, 1, 3.
0, 1, 5. Discarded.
0, 2, 6, 9.
0, 2, 6, 9, 13.
-----------------------------------------------------------------------------
A[13] = 11. Case 3. Clone, extend and discard.
0.
0, 1.
0, 1, 3.
0, 2, 6, 9.
0, 2, 6, 9, 11.
0, 2, 6, 9, 13. Discarded.
-----------------------------------------------------------------------------
A[14] = 7. Case 3. Clone, extend and discard.
0.
0, 1.
0, 1, 3.
0, 1, 3, 7.
0, 2, 6, 9. Discarded.
0, 2, 6, 9, 11.
----------------------------------------------------------------------------
A[15] = 15. Case 2. Clone and extend.
0.
0, 1.
0, 1, 3.
0, 1, 3, 7.
0, 2, 6, 9, 11.
0, 2, 6, 9, 11, 15. <-- LIS List
----------------------------------------------------------------------------
注:观察上面的处理过程,我们都只在处理所有active list的最后一个元素end element(粗体),那么仅仅需要维护所有active list构成的end element集合(粗体斜边),
可以用一维数组来存储。discard操作可以用replace操作来模拟。
四、算法实现
第三节的算法描述序号分别对应下面的算法实现
1、时间复杂度为O(n^2)的DP实现
1 /** 2 @description: Longest Increasing Subsequence 3 @author: seiyagoo 4 @create: 2013.10.25 5 @modified: 2013.10.26 6 **/ 7 int LIS_1(int A[], int size){ 8 9 int *LIS = new int[size]; 10 vector<int> *vec = new vector<int>[size]; 11 12 /* Compute optimized LIS values in bottom up manner */ 13 for(int i=0; i < size; i++){ 14 LIS[i]=1; //初始化默认长度 15 int max_j=0, flag=0; 16 for(int j=0; j < i; j++){ //查表,找出前面最长的序列, 若将A[i]加入LIS[j](LIS[j]+1的含义)的递增子序列比当前的LIS[i]更长, 则更新LIS[i] 17 if(A[i] > A[j] && LIS[i] < LIS[j]+1){ 18 LIS[i] = LIS[j]+1; 19 max_j=j; 20 flag=1; 21 } 22 } 23 if(flag) //copy前面最长子序列到vec[i] 24 vec[i].insert(vec[i].end(), vec[max_j].begin(), vec[max_j].end()); 25 vec[i].push_back(A[i]); //最后放入A[i] 26 } 27 28 /*Show LIS of the current state*/ 29 vector<int>::iterator it; 30 cout<<left; 31 for(int i=0; i<size; i++){ 32 cout<<setw(2)<<A[i]<< " --> "; 33 for(it = vec[i].begin(); it!=vec[i].end(); it++) 34 cout<<*it<<" "; 35 cout<<endl; 36 } 37 38 /* Pick maximum of all LIS values, namely max{LIS[i]} */ 39 int max_len=0; 40 for(int i = 0; i < size; i++ ) 41 if( max_len < LIS[i] ) 42 max_len = LIS[i]; 43 44 delete[] LIS; 45 delete[] vec; 46 47 return max_len; 48 }
2、时间复杂度为O(nlogn)的DP实现
1 /** 2 @description: Longest Increasing Subsequence 3 @author: seiyagoo 4 @create: 2013.10.25 5 @modified: 2013.10.26 6 **/ 7 8 // Binary search (note boundaries in the caller) 9 // A[] is ceilIndex in the caller 10 int CeilIndex(int A[], int l, int r, int key) { 11 int m; 12 13 while( r - l > 1 ) { 14 m = l + (r - l)/2; 15 (A[m] >= key ? r : l) = m; // ternary expression returns an l-value 16 } 17 18 return r; 19 } 20 21 int LIS_2(int A[], int size) { 22 // boundary case: when array size is one 23 if( 1 == size ) return 1; 24 25 int *tailTable = new int[size]; 26 vector<int> *vec = new vector<int>[size]; 27 int len; // always points empty slot 28 29 //memset(tailTable, INT_MAX, sizeof(tailTable[0])*size); @bug 30 31 for(int i = 0; i < size; i++) 32 tailTable[i] = INT_MAX; 33 34 tailTable[0] = A[0]; //tailTable[0] store the smallest value 35 vec[0].push_back(A[0]); 36 37 len = 1; 38 for( int i = 1; i < size; i++ ) { 39 if( A[i] < tailTable[0] ) { //case 1: new smallest value 40 tailTable[0] = A[i]; 41 42 /*discard and create*/ 43 vec[0].clear(); 44 vec[0].push_back(A[i]); 45 } 46 else if( A[i] > tailTable[len-1] ) { //case 2: A[i] wants to extend largest subsequence 47 tailTable[len++] = A[i]; 48 49 /*clone and extend*/ 50 vec[len-1] = vec[len-2]; 51 vec[len-1].push_back(A[i]); 52 } 53 else { //case 3: A[i] wants to be current end candidate of an existing subsequence, It will replace ceil value in tailTable 54 int ceilIndex = CeilIndex(tailTable, -1, len-1, A[i]); 55 tailTable[ceilIndex] = A[i]; 56 57 /*discard, clone and extend*/ 58 vec[ceilIndex].clear(); 59 vec[ceilIndex] = vec[ceilIndex-1]; 60 vec[ceilIndex].push_back(A[i]); 61 } 62 63 /*Printf all the active lists*/ 64 vector<int>::iterator it; 65 cout<<left; 66 cout<<"A["<<i<<"] = "<<A[i]<<endl<<endl; 67 cout<<"active lists:"<<endl; 68 for(int i=0; i<len; i++){ 69 for(it = vec[i].begin(); it!=vec[i].end(); it++) 70 cout<<*it<<" "; 71 cout<<endl; 72 } 73 74 /*Printf end elements of all the active lists*/ 75 cout<<endl<<"end elements array:"<<endl; 76 for(int i = 0; i < size; i++) 77 if(tailTable[i] != INT_MAX) 78 cout<<tailTable[i]<<" "; 79 cout<<endl; 80 cout<<"-------------------------"<<endl; 81 } 82 83 84 delete[] tailTable; 85 delete[] vec; 86 87 return len; 88 }
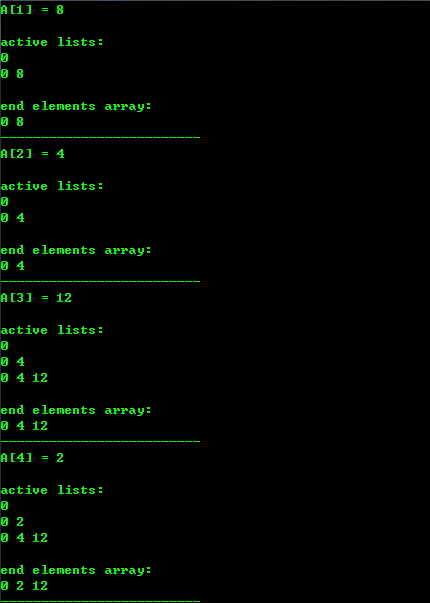
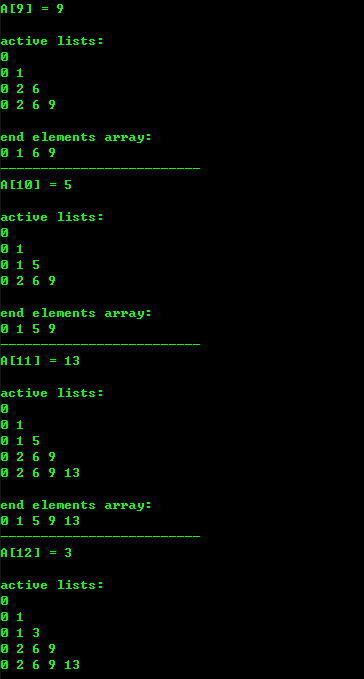
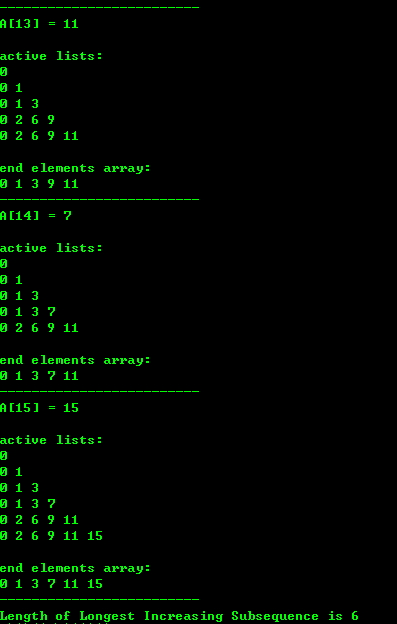
五、运行结果
example:
0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
算法实现一

算法实现二

参考:
《编程之美》