一、分类和回归的区别
we will focus on the binary classification problem in which y can take on only two values, 0 and 1分类产生结果为{0,1}


二、逻辑回归模型表示
sigmoid函数(逻辑函数)把假设值映射到一个在0-1之间的函数上:
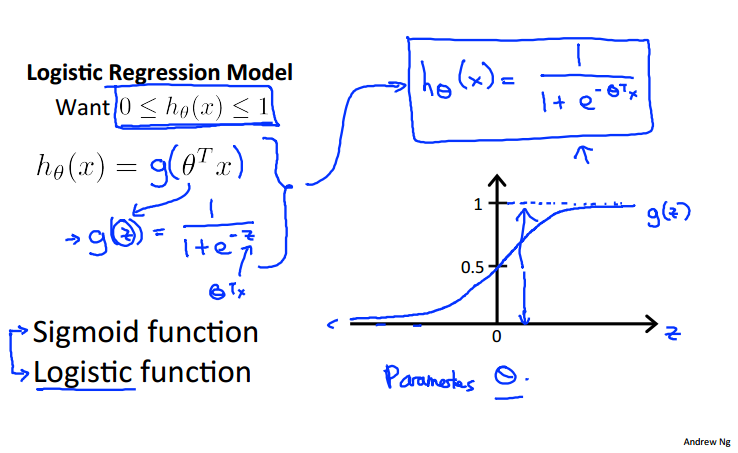

关于模型表示的解释,假设函数h预测的是输入x预测值为1的可能性(概率),例如当h为0.7的时候表示患者患有肿瘤的可能性是70%

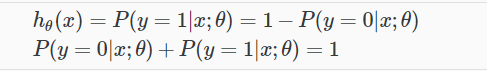
三、决策边界
当z>=0时y=1,当z<0时y=0
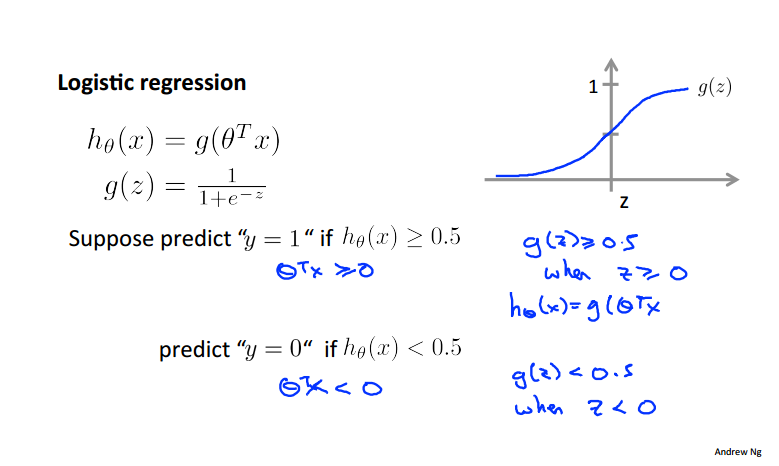

使g()中的表达式=0的这条线即为决策边界,也就是决定预测结果是0/1的边界线:
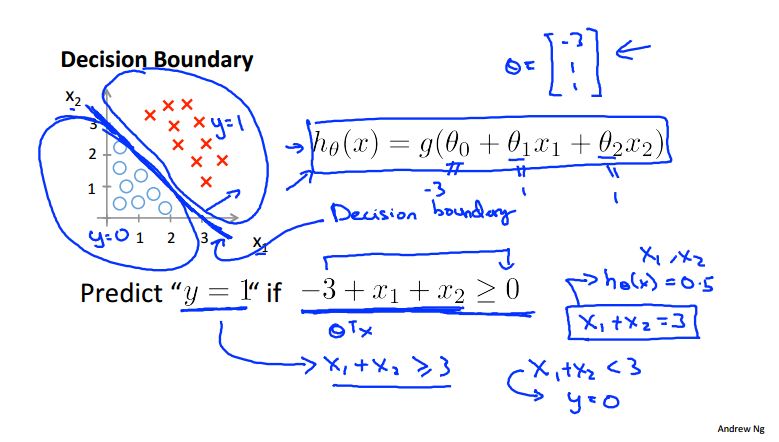
非线性的决策边界:

四、代价函数
我们不能使用线性回归中的代价函数,因为得出的曲线呈现波浪形,会产生很多个局部变量,而不是理想的凸型曲线:

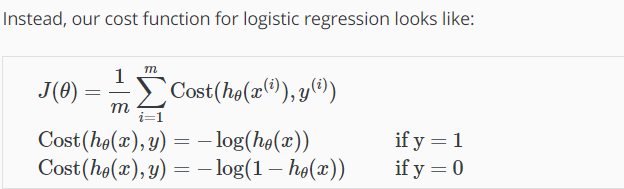
当y=1时,为递减函数,h越接近1,则代价越小,越接近0则代价趋近于无穷大:

y=0时则与之相反,h越接近0时代价越小:
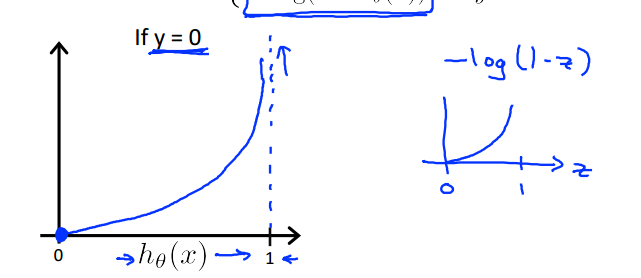
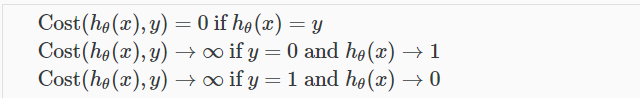
五、优化目标

向量化的表示方法:

奇妙的是梯度下降法中求代价函数的梯度值居然与线性回归一模一一样!

向量化的表示方法:

六、高级优化方法

MATLAB自带函数工具包计算方法:

function [jVal, gradient] = costFunction(theta) jVal = [...code to compute J(theta)...]; gradient = [...code to compute derivative of J(theta)...]; end
options = optimset('GradObj', 'on', 'MaxIter', 100); initialTheta = zeros(2,1); [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
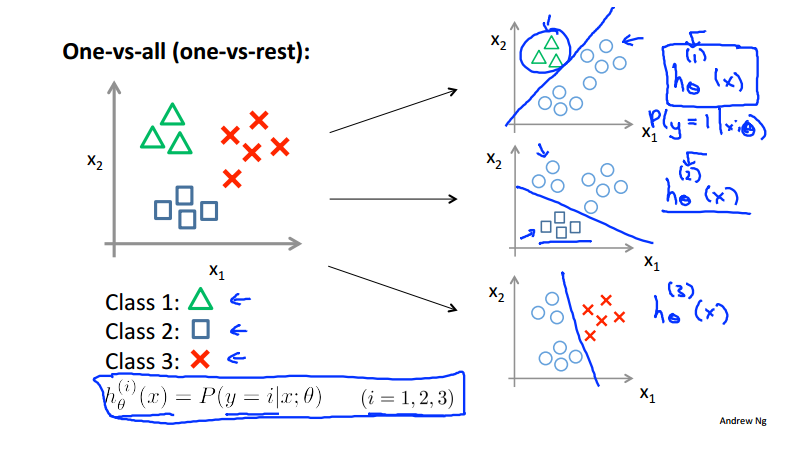
七、多分类问题
和二分类思想相似,这里有三类便进行三次二分类,计算出每次的概率值,最大值即为我们在多个类别中最终预测出来的值:

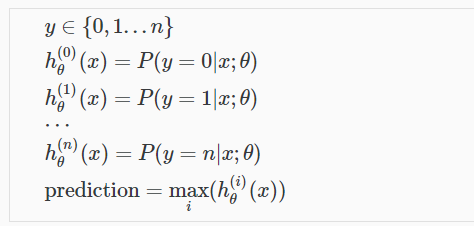
八、过拟合问题 overfitting
underfitting—in which the data clearly shows structure not captured by the model—and the figure on the right is an example of overfitting.学习地不好和学习地太好(忽略了generalization):
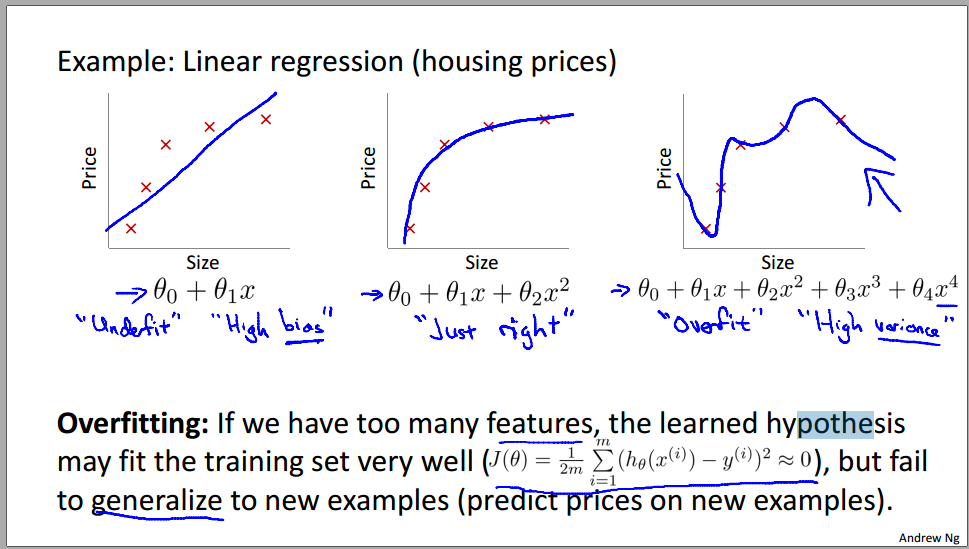
解决过拟合的两种方法1:减少特征变量的数目 2:降低参数的值,让每个特征变量只贡献一点点

九、正则化
消除θ3和4的影响,把它们对应的参数设置地很大:
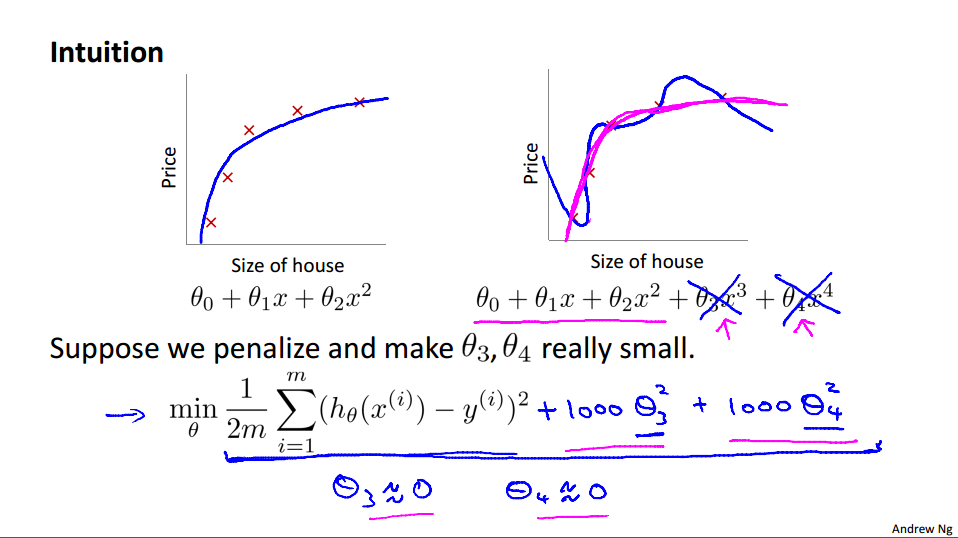

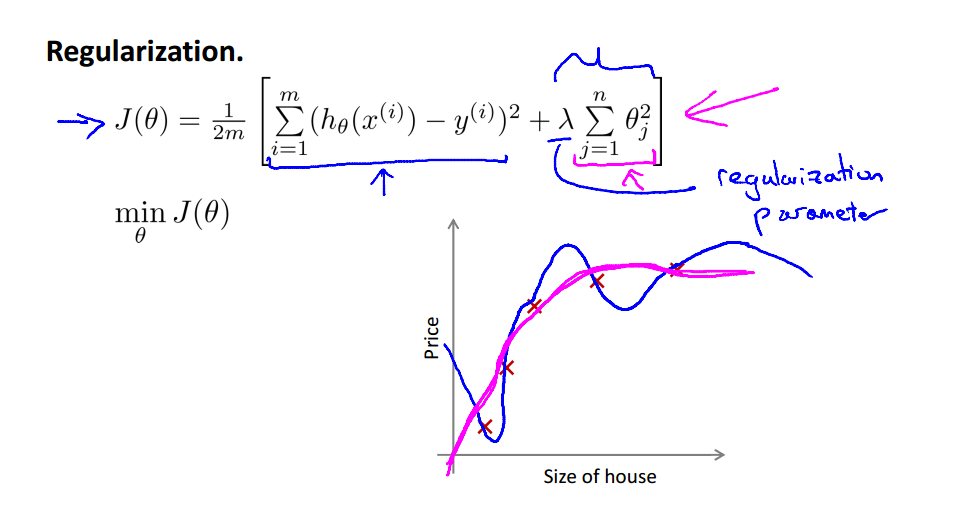

λ设置的非常大的后果:


梯度下降法的求解过程:


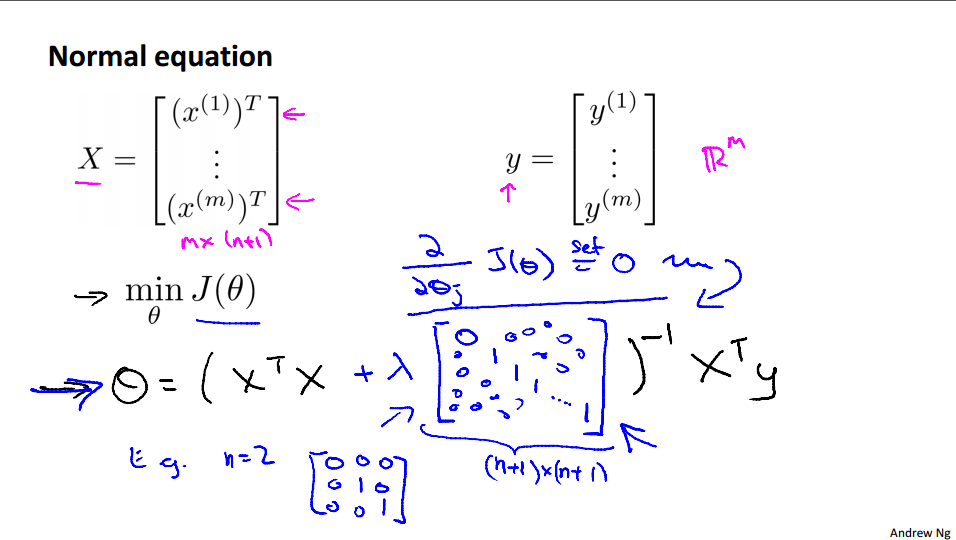
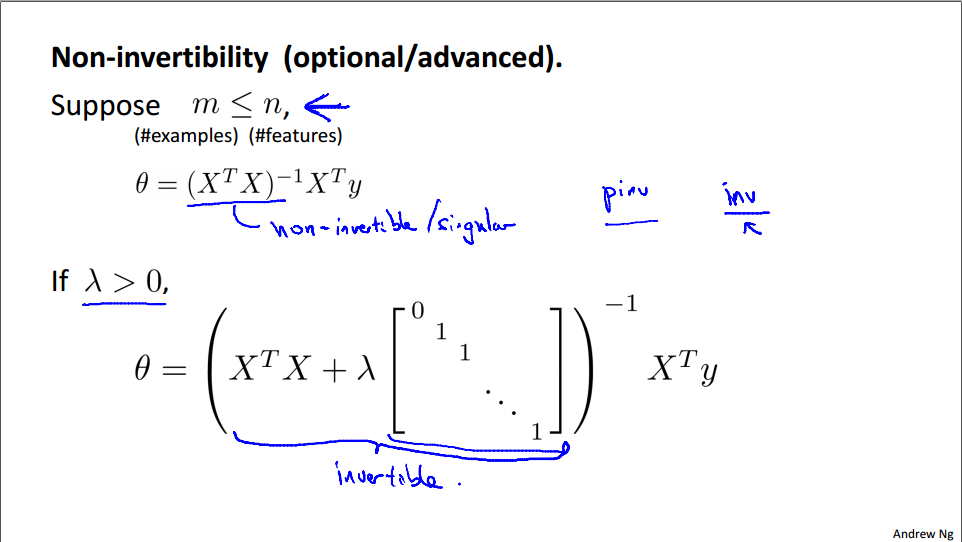
正规方程(可逆和不可逆的情况)

十、正规化逻辑斯特回归
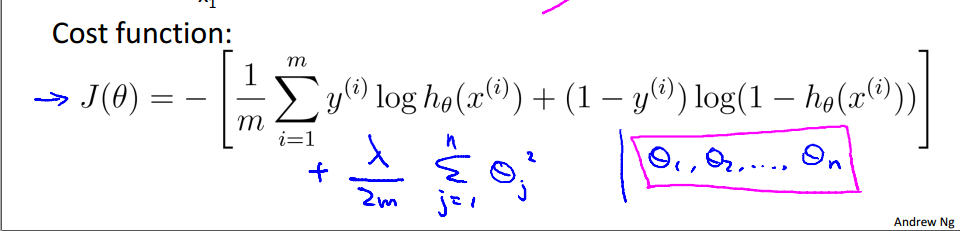
梯度下降法:

