利用Matla绘制多元函数的梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
下面在matlab里绘制空间曲面,曲面的等高线图,以及各曲面上各个网格点的梯度(向量)
首先,基于Matlab,绘制函数Z=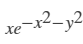 的图形:
的图形:
1 [X,Y] = meshgrid(-2:0.2:2); %生成数据网格点 2 Z = X .* exp(-X.^2 - Y.^2); %计算所有网格点的数值 3 surfc(Z);%绘制三维函数图像

然后, 在matlab中使用 hold 函数合并等高线图和箭头图:
沿 x 和 y 方向在从 -2 到 2 的网格上绘制 10 条 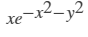 等高线。
等高线。
1 [X,Y] = meshgrid(-2:0.2:2); 2 Z = X .* exp(-X.^2 - Y.^2); 3 contour(X,Y,Z,10)
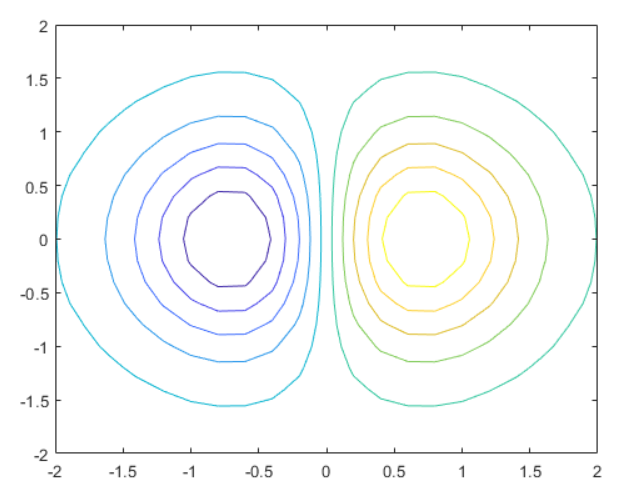
最后,使用 gradient 函数计算 Z 的二维梯度。gradient 函数会返回 U 作为 x 方向上的梯度,返回 V 作为 y 方向上的梯度。使用 quiver 函数显示指示梯度值的箭头。
1 [U,V] = gradient(Z,0.2,0.2); 2 hold on 3 quiver(X,Y,U,V) 4 hold off
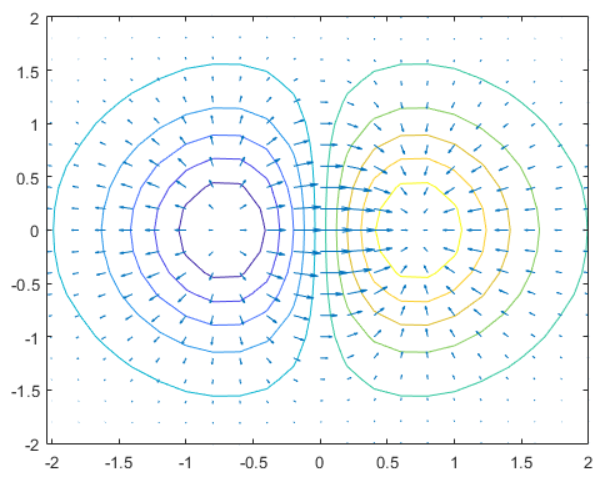
从图中可以看出,梯度本质就是向量,向量的方向垂直于曲面的等高线,并且指向高度增加方向的向量(箭头的指向,从地势低洼处指向地势较高的位置,且函数变化最快的方向)