语谱图
生成语谱图的前提:
在一段时间内(如10~30ms,即所谓一帧内)可以认为频谱是不变的。【blog链接】
如何理解在一段时间内频谱是不变的?
先看图:
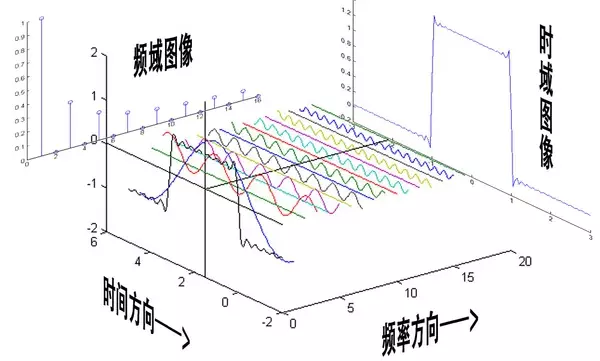
上图引自《傅里叶变换终极解释》
理解:对于频率方向上的若干个频率,当在时间方向上前进一段10-30ms的距离时,我们可以认为这些个频率对应的振幅不变。(时间太短,振幅还没变化。)
所以如果帧长时间太长,则这些个频率对应的振幅可能是有变化的。此时若再放在一帧里面表示则不能精确地刻画各个频率随时间变化的振幅值。
语谱图生成流程
引自blog:《语音信号处理之(四)梅尔频率倒谱系数(MFCC)》
我们处理的是语音信号,那么如何去描述它很重要。因为不同的描述方式放映它不同的信息。那怎样的描述方式才利于我们观测,利于我们理解呢?这里我们先来了解一个叫声谱图的东西。
这里,这段语音被分为很多帧,每帧语音都对应于一个频谱(通过短时FFT计算),频谱表示频率与能量的关系。在实际使用中,频谱图有三种,即线性振幅谱、对数振幅谱、自功率谱(对数振幅谱中各谱线的振幅都作了对数计算,所以其纵坐标的单位是dB(分贝)【关于分贝的理解】。这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高,以便观察掩盖在低幅噪声中的周期信号)。
我们先将其中一帧语音的频谱通过坐标表示出来,如上图左。现在我们将左边的频谱旋转90度。得到中间的图。然后把这些幅度映射到一个灰度级表示(也可以理解为将连续的幅度量化为256个量化值?),0表示黑,255表示白色。幅度值越大,相应的区域越黑。这样就得到了最右边的图。那为什么要这样呢?为的是增加时间这个维度,这样就可以显示一段语音而不是一帧语音的频谱,而且可以直观的看到静态和动态的信息。优点稍后呈上。
这样我们会得到一个随着时间变化的频谱图,这个就是描述语音信号的spectrogram声谱图。
下图是一段语音的声谱图,很黑的地方就是频谱图中的峰值(共振峰formants)。
那我们为什么要在声谱图中表示语音呢?
首先,音素(Phones)的属性可以更好的在这里面观察出来。另外,通过观察共振峰和它们的转变可以更好的识别声音。隐马尔科夫模型(Hidden Markov Models)就是隐含地对声谱图进行建模以达到好的识别性能。还有一个作用就是它可以直观的评估TTS系统(text to speech)的好坏,直接对比合成的语音和自然的语音声谱图的匹配度即可。
总结:
对于一段语音信号x(t),
(1)首先分帧,变为x(m,n)(n为帧长,m为帧的个数);
(2)然后做FFT变换,得到X(m,n),做周期图Y(m,n)(Y(m,n) = X(m,n) * X(m,n)');
(3)接着取10 *log10(Y(m,n)),把m根据时间变换一下刻度M,n根据频率变化一下刻度N;
(4)最后将(M,N, 10*log10(Y(m,n) 画成二维图就是语谱图了。
共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。复数z的共轭复数记作zˊ。
z· z′=|z|2=a2+b2(实数);
在matlab中conj(x)是求x的共轭数。
问题:
序列的DFT的输出是什么?
一个序列可以看成是一个函数。比如序列 [a,b,c,d],可以看成是一个函数f(x)在x=1,2,3,4出分别取值a,b,c,d。
由于任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。
那么对该序列做DFT的意义就是找出这个函数f(x)是由哪些振幅和频率的正弦余弦函数构成的。
参考链接
http://old.sebug.net/paper/books/scipydoc/frequency_process.html
参考书籍:
王永琦. MATLAB与音视频技术[M]. 清华大学出版社, 2013. P125
梁瑞宇, 赵力, 魏昕. 语音信号处理实验教程[M]. 机械工业出版社, 2016. P60



