1:快速幂
问题如下:
求 a^n % m 的值是多少?n是1到10^18次方的一个整数。
求一个数的n次方,朴素的算法就是直接for循环,O(N)的复杂度。
但是对于这个问题n实在是太大了,O(N)也会超时,那么需要更快的算法,快速幂算法。
要求 a^n,如果知道了 a^(n/2) 次方的话,再来个平方就可以了。
那么按照这个思路就能运用分治的思想了。
代码如下:
//用递归有可能爆栈出错
LL qsm(LL a, LL n, LL m){
LL ans = 1;
while(n>0){
if(n&1){
ans = (a*ans)%m;
}
a = (a*a)%m;
n>>=1;
}
return ans;
}
2.矩阵快速幂
问题如下:
f(1)=1, f(2)=1 , f(n)=a*f(n-1)+b*f(n-2),输出n和m,求 f(n) % m 的值。n是1到10^18次方的数。
朴素的想法同上,直接一个for循环递推过去,这样复杂度是O(N)的,还是比较慢。
然后想到高中的数学问题,用特征方程求这个递推式的非递推通项方程,求出是 f(n)=c1*x1^n+c2*x2^n ,这样的话应用前面的快速幂就可以求解了。
但是x1和x2大部分情况是小数,这是求出来会有误差而且没法取模,并不能算出精确值来。
考虑矩阵这种数学工具,构造矩阵:
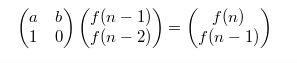
则求 f(n) 的话如下:
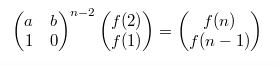
那么只要用快速幂求出矩阵的n-2次方来,因为都是整数,所以不会有精度问题,也就得到了正确答案。
也就是矩阵快速幂。
代码如下:
#include <cstdio> #include <string> #include <cmath> #include <iostream> using namespace std; const long long M = 1000007; const long long N = 3; long long t,b,c,f1,f2; struct Node //矩阵 { long long line,cal; long long a[N+1][N+1]; Node(){ line=3,cal=3; a[0][0] = b; a[0][1] = 1; a[0][2] = 0; a[1][0] = t; a[1][1] = 0; a[1][2] = 0; a[2][0] = c; a[2][1] = 0; a[2][2] = 1; } }; Node isit(Node x,long long c) //矩阵初始化 { for(long long i=0;i<N;i++) for(long long j=0;j<N;j++) x.a[i][j]=c; return x; } Node Matlab(Node x,Node s) //矩阵乘法 { Node ans; ans.line = x.line,ans.cal = s.cal; ans=isit(ans,0); for(long long i=0;i<x.line;i++) { for(long long j=0;j<x.cal;j++) { for(long long k=0;k<s.cal;k++) { ans.a[i][j] += x.a[i][k]*s.a[k][j]; ans.a[i][j]=(ans.a[i][j]+M)%M; } } } return ans; } long long Fast_Matrax(long long n) //矩阵快速幂 { if(n==1) return f1; n-=2; long long x=1,f=n,ok=1; Node ans,tmp,ch; ans.line = 1,ans.cal = 3; ans.a[0][0] = f2, ans.a[0][1] = f1 ,ans.a[0][2] = 1; while(n>0) { if(n%2) { ans=Matlab(ans,tmp); } tmp=Matlab(tmp,tmp); n/=2; } return ans.a[0][0]; } int main() { long long n,T; scanf("%lld",&T); while(T--) { scanf("%lld%lld%lld%lld%lld%lld",&f1,&f2,&t,&b,&c,&n); printf("%lld ",Fast_Matrax(n)); } return 0; }
3.快速乘(当longlong都无法装下的时候)
问题:
求 (a*b) % m 的值,其中 a,b,m 是1到10^18。
如果直接乘的话,因为a和b还有m都很大,那么会溢出long long,所以需要一些方法。
朴素的想法是用数组模拟高精度,但是比较麻烦。
还有更好的方法:
求乘法的列竖式,
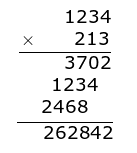
1234*213=1234*3+1234*10*1+1234*10^2*2;
那么如果变成二进制的话 10101 × 1011 = 10101*1+10101*2^1*1+10101*2^2*0+10101*2^3*1;
这样代码如下:
long long q_mul( long long a, long long b, long long mod ) //快速计算 (a*b) % mod { long long ans = 0; // 初始化 while(b) //根据b的每一位看加不加当前a { if(b & 1) //如果当前位为1 { b--; //也可不要,方便理解而已 ans =(ans+ a)%mod; //ans+=a } b /= 2; //b向前移位 a = (a + a) % mod; //更新a } return ans; }
就是模拟了二进制的竖式乘法,因为每次最多×2,所以不会溢出。
这样的复杂度是 logN 的。