树堆,在数据结构中也称Treap,是指有一个随机附加域满足堆的性质的二叉搜索树,其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树,Treap的特点是实现简单,且能基本实现随机平衡的结构。
在深入了解Treap之前,我们先来了解一下BST。
BST(Binary-search tree),即二分搜索树,是一棵二叉树,且满足性质:若每个节点都有一个key值,则对于每个根节点,均满足key[leftson]<key[root]<key[rightson]。换句话说,即满足树的先序遍历等于树的中序遍历。如下图即为一颗BST:
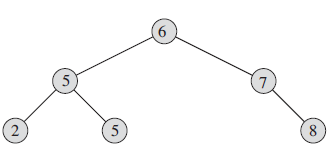
其特点可以帮助我们快速查找树中的某些元素。举个例子,如果我们要查找2元素,那么先与6比较,比6小,那么进入6的左子树,再与5进行比较,比5小,进入5的左子树,我们就成功地找到了2。这比我们暴力查找要快得多。但是缺点也很显著。比如说,如果输入数据满足单调递增性质,那么我们在建树时便会将其建成一条链,从而导致其算法的复杂度退化。当然,特定情况下,我们可以借助random—shuffle函数将数据打乱,但是一般情况下,BST便有着很大的局限性。因此我们需要一种更高级的数据结构来克服这种局限性,便是我们的Treap。
Treap=Tree+heap,顾名思义,Treap便是一种树与堆的结合体。总的来说,就是在维护BST性质的同时,给与每个节点一个随机的random值,同时保证random值满足小根堆的性质。这样,便可以轻而易举的防止复杂度的退化。
在了解了Treap的原理之后,我们便可以尝试用代码来实现其功能。下面以洛谷-P3369普通平衡树为例,一道典型并且操作齐全的模版题,其主要要求我们完成6个操作:
-
插入x数
-
删除x数(若有多个相同的数,因只删除一个)
-
查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数,因输出最小的排名)
-
查询排名为x的数
-
求x的前驱(前驱定义为小于x,且最大的数)
-
求x的后继(后继定义为大于x,且最小的数)
首先便是随机值的实现。由于<stdlib>中的rand()函数速度较慢且局限性较大,在数据结构中不太适用,所以在这里建议rand函数的功能用手写来实现。
随机函数:
int rand()
{ int seed=12345; return seed=(int)seed*482711LL%2147483647; }
稍微优化后可以变为这样(虽然没什么用):
inline int rand()
{ static int seed=12345; return seed=(int)seed*482711LL%2147483647; }
然后还需要一个函数来更新每个节点的信息,也是十分的浅显易懂:
void update(int p) { size[p]=size[l[p]]+size[r[p]]+ct[p]; }
在我们维护Treap的过程中,子树大小的维护也时时刻刻都是有必要的,在每个函数中都应该有体现,具体维护方式如下:
对于旋转,我们要在旋转后对子节点和根节点分别重新计算其子树的大小。
对于插入,在寻找插入的位置时,每经过一个节点,都要先使以它为根的子树的大小增加 1,再递归进入子树查找。
对于删除,在寻找待删除节点,递归返回时要把所有的经过的节点的子树的大小减少 1。要注意的是,删除之前一定要保证待删除节点存在于 Treap 中。
维护子树的大小也是Treap的一个关键部分。
那么现在便来到了最关键也是Treap中最核心的一步:如何维护堆的性质,即如何在Treap中插入元素(ins)。
对于Treap中的每个元素,为保证我们堆的性质,插入操作便分为了两种操作:左旋(lturn),右旋(rturn)。下面重点讲解这两种操作。
下面画了一个图以便理解:
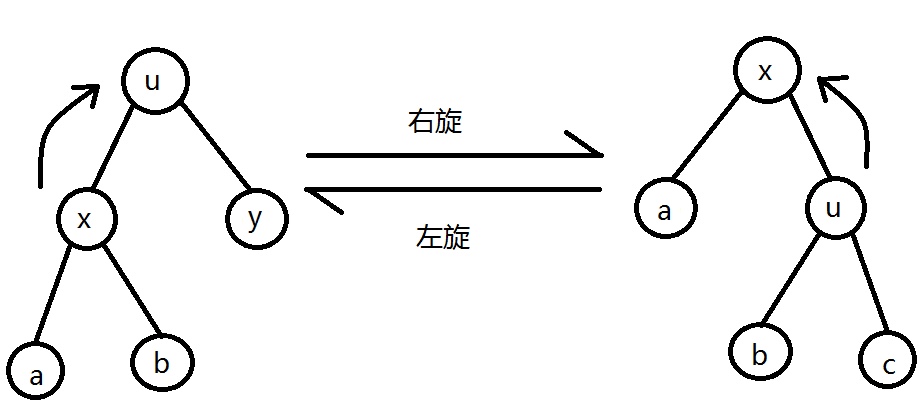
以上图为例,我们可以看到,从左到右便是右旋的过程,使得根节点由u变为了x。由于a仍比x小,所以x的左子树仍为a,u比x大,所以为x的右子树,但对于b,大于x小于u,所以应在x的右子树,u的左子树,同理,c应在u的右子树,旋转完毕。这便是右旋的过程。
理解了右旋的过程之后,我们也可以较为轻松的写出右旋的代码,为了方便,加了个小小的传引用:
void rturn(int &k) { int t=l[k];//记录左儿子 l[k]=r[t]; r[t]=k;//旋转的过程 size[t]=size[k];//size的转换 update(k);//更新k k=t; }
左旋转的过程就是上图从右到作的过程,代码实现也同理:
void lturn(int &k) { int t=r[k];//记录右儿子 r[k]=l[t]; l[t]=k;//旋转 size[t]=size[k];///size转换 update(k);//更新k k=t; }
了解这两种操作后,插入元素就变得得心应手了,先把要插入的点插入到一个叶子上,然后跟维护堆一样,如果当前节点的优先级比根大就旋转,如果当前节点是根的左儿子就右旋,如果当前节点是根的右儿子就左旋。
依然举两个例子来帮助理解:
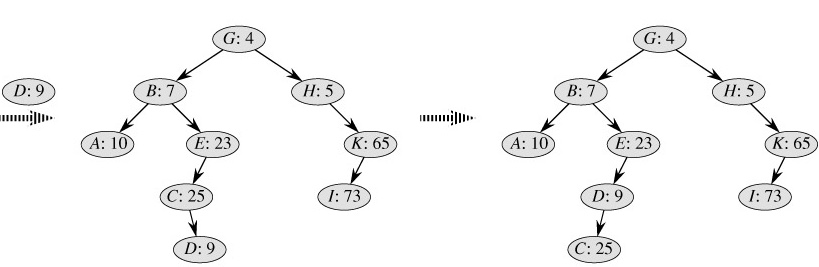
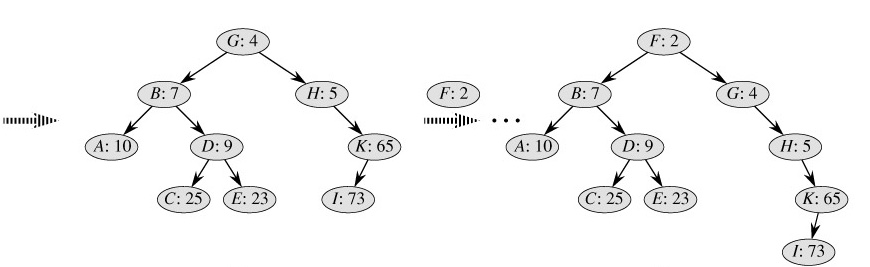
如图所示,我们需要把D和F元素插入到Treap中,对于D,先将其放在一个叶子节点,然后与其父亲相比较发现比父亲小却在父亲的右子树上,所以我们需要对D进行右旋操作,同理,F元素经过一次次的比较,一次次的旋转,最终也可以到达如图所示的位置。
至此,我们已经基本解决了对于Treap的插入操作。
代码如下:
void ins(int &p,int x) { if (p==0) { p=++sz; size[p]=ct[p]=1,v[p]=x,rnd[p]=rand(); return; } size[p]++; if (v[p]==x) ct[p]++; else if (x>v[p]) { ins(r[p],x); if (rnd[r[p]]<rnd[p]) lturn(p); } else { ins(l[p],x); if (rnd[l[p]]<rnd[p]) rturn(p); } }
接下来是删除操作(del),删除操作算是Treap中最难理解的操作了吧(主要因为代码长╮(╯▽╰)╭)。本可以通过两种方式来达成删除操作,但对于初学者来讲,这里推荐并主要讲解其中一种方式。
注意到Treap的性质,即必须满足堆的性质,所以对于Treap,我们也可以用删除堆的方式,借助旋转操作,加以解决。
如果该节点的左子节点的key小于右子节点的key,右旋该节点,使该节点降为右子树的根节点,然后访问右子树的根节点,递归地操作下去;反之同理。实质上即为让key小的节点有限旋到上面,保证堆的性质,进而进行删除操作。
删除操作比较难以理解,希望通过代码可以加深对其的认识。
代码实现:
void del(int &p,int x) { if (p==0) return; if (v[p]==x) { if (ct[p]>1) ct[p]--,size[p]--; else { if (l[p]==0||r[p]==0) p=l[p]+r[p]; else if (rnd[l[p]]<rnd[r[p]]) rturn(p),del(p,x); else lturn(p),del(p,x); } } else if (x>v[p]) size[p]--,del(r[p],x); else size[p]--,del(l[p],x); }
解决完删除操作后,查找(query)操作便显得较为简单,按照一般树上问题解决方式统计即可,这里不多赘述,其中query1代表查询x数的排名,query2代表查询排名为x的数。
代码实现:
int query1(int p,int x) { if (p==0) return 0; if (v[p]==x) return size[l[p]]+1; if (x>v[p]) return size[l[p]]+ct[p]+query1(r[p],x); else return query1(l[p],x); }
int query2(int p,int x) { if (p==0) return 0; if (x<=size[l[p]]) return query2(l[p],x); x-=size[l[p]]; if (x<=ct[p]) return v[p]; x-=ct[p]; return query2(r[p],x); }
最后,我们来处理一下前驱与后继的问题。前驱定义为小于x,且最大的数,后继定义为大于x,且最小的数,也较为简单,过程中维护一下max和min即可轻易地解决。
该部分代码:
int findfront(int p,int x) { if (p==0) return -inf; if (v[p]<x) return max(v[p],findfront(r[p],x)); else if (v[p]>=x) return findfront(l[p],x); }
int findback(int p,int x) { if (p==0) return inf; if (v[p]<=x) return findback(r[p],x); else return min(v[p],findback(l[p],x)); }
至此,Treap中的所有操作都已经解决。将这些操作拼接串联起来,便构成了Treap的基本框架,完整模版如下(以普通平衡树为例):
#include <stdio.h> #include <algorithm> #include <stdlib.h> using namespace std; #define inf 300000030 int l[100100],r[100100],v[100100],size[100100],rnd[100100],ct[100100]; int sz; void update(int p) { size[p]=size[l[p]]+size[r[p]]+ct[p]; } void lturn(int &k) { int t=r[k]; r[k]=l[t]; l[t]=k; size[t]=size[k]; update(k); k=t; } void rturn(int &k) { int t=l[k]; l[k]=r[t]; r[t]=k; size[t]=size[k]; update(k); k=t; } void ins(int &p,int x) { if (p==0) { p=++sz; size[p]=ct[p]=1,v[p]=x,rnd[p]=rand(); return; } size[p]++; if (v[p]==x) ct[p]++; else if (x>v[p]) { ins(r[p],x); if (rnd[r[p]]<rnd[p]) lturn(p); } else { ins(l[p],x); if (rnd[l[p]]<rnd[p]) rturn(p); } } void del(int &p,int x) { if (p==0) return; if (v[p]==x) { if (ct[p]>1) ct[p]--,size[p]--; else { if (l[p]==0||r[p]==0) p=l[p]+r[p]; else if (rnd[l[p]]<rnd[r[p]]) rturn(p),del(p,x); else lturn(p),del(p,x); } } else if (x>v[p]) size[p]--,del(r[p],x); else size[p]--,del(l[p],x); } int query1(int p,int x) { if (p==0) return 0; if (v[p]==x) return size[l[p]]+1; if (x>v[p]) return size[l[p]]+ct[p]+query1(r[p],x); else return query1(l[p],x); } int query2(int p,int x) { if (p==0) return 0; if (x<=size[l[p]]) return query2(l[p],x); x-=size[l[p]]; if (x<=ct[p]) return v[p]; x-=ct[p]; return query2(r[p],x); } int findfront(int p,int x) { if (p==0) return -inf; if (v[p]<x) return max(v[p],findfront(r[p],x)); else if (v[p]>=x) return findfront(l[p],x); } int findback(int p,int x) { if (p==0) return inf; if (v[p]<=x) return findback(r[p],x); else return min(v[p],findback(l[p],x)); } int ss; int main() { int n; scanf("%d",&n); for(int i=1;i<=n;i++) { int flag,x; scanf("%d%d",&flag,&x); if (flag==1) ins(ss,x); if (flag==2) del(ss,x); if (flag==3) printf("%d\n",query1(ss,x)); if (flag==4) printf("%d\n",query2(ss,x)); if (flag==5) printf("%d\n",findfront(ss,x)); if (flag==6) printf("%d\n",findback(ss,x)); } }