求解多边形面积2S= Σ【Xi （Yi+1-Yi-1）】,（i属于1~n），公式解析及编程实现

    yogurt今天要个大家分享一个基础的二维空间多边形面积求算方法，主要也是为了之后一篇《椭球体上某区域面积的求算，及兰伯特投影与墨卡托投影后该区域面积对比》打一个基础。关于投影的相关过程及编程方法，大家可以参考我之前写过的《.gen地图文件的投影编程实现（以墨卡托投影和兰伯特投影为例）》http://www.cnblogs.com/to-sunshine/p/6048438.html。

    下面和大家分析一下算法思路吧：

==========================yogurt小课堂开课了=========================

    首先，我们知道一个二维多边形可以被分解成多个三角形，多边形的面积即为所有三角形的面积之和了。然后就是怎么将求解三角形的面积与坐标点联系起来了，因为我们在程序中只给出了多边形每个点的坐标而已，这和我们手动计算不一样，毕竟计算机可没这么智能。

    三角形的面积 S = 1/2 a X h，这里假设a为三角形的底边长，h为三角形的高。那么这里 h  =b X sin夹角 ，这样便让求取面积相关因子变到了三角形的边和夹角上。即 S = 1/2 a X b X sin夹角。看到这里相信聪明的你一定看出来了，a X b X sin夹角，很眼熟啊！对，它等于 | 向量a X 向量b | ，自然而然的，向量便把几何的图形与点坐标联系起来了。

    所以，三角形的面积 S = 1/2 | 向量a X 向量b | ，而 | 向量a X 向量b | = X1Y2 - X2Y1 ，如果想要把两条边的交点看做原点的话，那么 | 向量a X 向量b | =（Xa-Xo）（Yb-Yo）- （Xb-Xo）（Ya-Yo）。为了不让分数参与运算，等式两边同时乘2，得到 2S = （Xa-Xo）（Yb-Yo）- （Xb-Xo）（Ya-Yo）。

    然后，我们假设在多边形外面有一个点P，多边形有N个顶点（V0~Vn-1）。要知道n-1是多边形的最后一个顶点，那么Vn就是V0，Vn+1就是V1。

    多边形的每两个点与这个P点相连都可以组成一个三角形，你会发现，从前一个点到后一个点是顺时针方向时，这个三角形面积为正的话，那么当从前一个点到后一个点是逆时针方向时，三角形面积为负。当正负相抵后，剩下的正好就是多边形的面积！如下图：

        因此，得到多边形面积 2S = 三角形（PV0V1） + 三角形（PV1V2） + …… + 三角形（PVn-2Vn-1） + 三角形（PVn-1V0）。

    为了方便计算三角形的面积，我们选择P点坐标为（0,0），那么 2S =【 Σ三角形（PViVi+1）】+ 三角形（PVi+1V0）,（i属于0到n-2）。下面就有一个比较复杂的换算工作，是为了简化等式，方便计算：

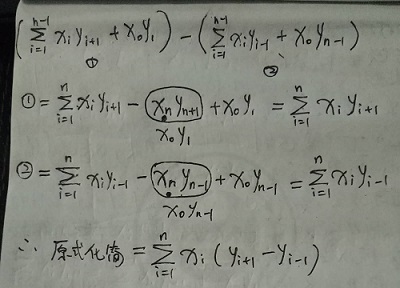
          最后，我们得到 2S = Σ【Xi （Yi+1-Yi-1）】,（i属于1~n）。

=================================下课了================================

    原理讲完啦，下面来给大家附上求解多边形面积的代码：

    假设第一个多边形几个顶点坐标分别是(4,6), (4,-4), (8, -4), (8,-8), (-4, -8), (-4,6), (4,6)，用未化简得公式求解；第二个多边形的几个顶点坐标分别是(3,4), (5,11), (12,8), (9,5), (5,6)，用化简后的公式求解。

// area.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include<math.h>

typedef struct
{
    int x,y;
}point;

int _tmain(int argc, _TCHAR* argv[])
{
    point p[7];
    p[0].x=4;p[0].y=6;
    p[1].x=4;p[1].y=-4;
    p[2].x=8;p[2].y=-4;
    p[3].x=8;p[3].y=-8;
    p[4].x=-4;p[4].y=-8;
    p[5].x=-4;p[5].y=6;
    p[6].x=4;p[6].y=6;

    int area=0;
    for(int i=0;i<6;i++)
    {
        area+=(p[i].x+p[i+1].x)*(p[i+1].y-p[i].y);
    }
    area =abs(area/2);
    printf("The area of graph1 is %d",area);

    point p2[6];
    p2[0].x = 3; p2[0].y = 4;
    p2[1].x = 5; p2[1].y = 11;
    p2[2].x = 12;p2[2].y = 8;
    p2[3].x = 9; p2[3].y = 5;
    p2[4].x = 5; p2[4].y = 6;
    p2[5].x = 3; p2[5].y = 4;

    int area2 = 0;
    for (int j = 0; j<5; j++)
    {
        area2 += (p2[j].x + p2[j + 1].x)*(p2[j + 1].y - p2[j].y);
    }
    
    area2 = abs(area2 / 2);
    printf("
The area of graph2 is %d", area2);

    return 0;
}

     结果如下：

     大家也可以手动验证一下，程序计算的对不对~~