(a) Draw the control flow graph for the printPrimes() method.
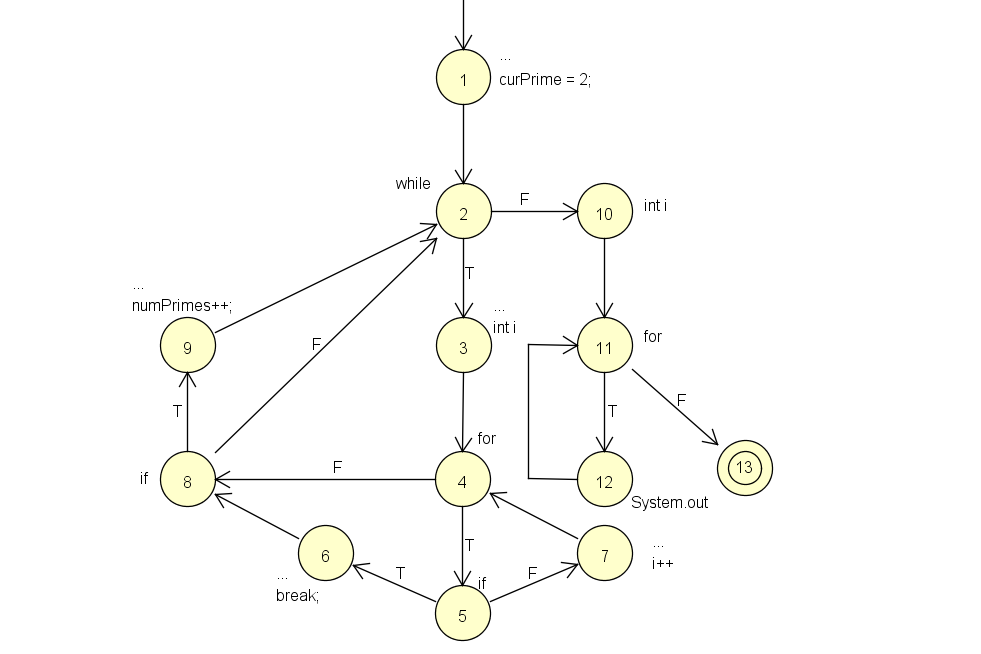
(b) Consider test cases t1 = ( n = 3 ) and t2 = ( n = 5 ).Design a simple fault that t2 would be more likely to discover than t1 would.
When MAXPRIMES is greater than less 5 but greater than 2, t2 would discover the out of bounds fault which t1 would not discover.
(c)Find a test case visits the edge that connects the beginning of the while statement to the for statement without going through they body of the while loop.
When n = 0, it would not go through the while body.
(d)Enumerate the TR for node coverage,edge coverage and prime path coverage for the graph.
NC: TR={1,2,3,4,5,6,7,8,9,10,11,12,13};
EC: TR={(1,2),(2,3),(2,10),(3,4),(4,5),(4,8),(5,6),(5,7),(6,8),(7,4),(8,2),(8,9),(9,2),(10,11),(11,12),(11,13),(12,11)};
PPC: TR={(1,2,3,4,8,9),(1,2,3,4,5,7),(1,2,3,4,5,6,8,9),(1,2,10,11,12),(1,2,10,11,13),(2,3,4,8,9,2),(2,3,4,8,2),(2,3,4,5,7),(2,3,4,5,6,8,9,2),(2,3,4,5,6,8,2),(2,10,11,12),(2,10,11,13),(3,4,5,6,8,9,2,3),(3,4,5,6,8,2,3),(3,4,8,9,2,3),(3,4,8,2,3),(3,4,5,6,8,9,2,10,11,12),(3,4,5,6,8,2,10,11,12),(3,4,5,6,8,9,2,10,11,13),(3,4,5,6,8,2,10,11,13),(3,4,8,9,2,10,11,12),(3,4,8,2,10,11,12),(3,4,8,9,2,10,11,13),(3,4,8,2,10,11,13),(4,5,7,4),(4,5,6,8,9,2,3,4),(4,5,6,8,2,3,4),(4,8,9,2,3,4),(4,8,2,3,4),(5,7,4,5),(5,6,8,9,2,3,4,5),(5,6,8,2,3,4,5),(6,8,9,2,3,4,5,6),(6,8,9,2,3,4,5,6),(6,8,9,2,3,4,5,7),(6,8,2,3,4,5,7),(7,4,5,7),(7,4,8,9,2,3),(7,4,8,2,3),(7,4,5,6,8,9,2,3),(7,4,5,6,8,2,3),(7,4,5,6,8,9,2,10,11,12),(7,4,5,6,8,9,2,10,11,13),(7,4,5,6,8,2,10,11,12),(7,4,5,6,8,2,10,11,13),(7,4,8,9,2,10,11,12),(7,4,8,9,2,10,11,13),(7,4,8,2,10,11,12),(7,4,8,2,10,11,13),(8,2,3,4,8),(8,9,2,3,4,8),(8,2,3,4,5,6,8),(8,9,2,3,4,5,6,8),(9,2,3,4,8,9),(9,2,3,4,5,6,8,9),(11,12,11),(12,11,12),(12,11,13)}.
SubMission:Test a prime path of the method by using JUint and EclEmma.
First add the isDivisable() method and alter the printPrimes() method. Put the output into an int array :
public class Prime { private static final int MAXPRIMES = 100; /******************************************************* * Finds and prints n prime integers * Jeff Offutt, Spring 2003 ******************************************************/ public static int[] printPrimes (int n) { int curPrime; // Value currently considered for primeness int numPrimes; // Number of primes found so far. boolean isPrime; // Is curPrime prime? int [] primes = new int [MAXPRIMES]; // The list of prime numbers. // Initialize 2 into the list of primes. primes [0] = 2; numPrimes = 1; curPrime = 2; while (numPrimes < n) { curPrime++; // next number to consider ... isPrime = true; for (int i = 0; i <= numPrimes-1; i++) { // for each previous prime. if (isDivisable(primes[i],curPrime)) { // Found a divisor, curPrime is not prime. isPrime = false; break; // out of loop through primes. } } if (isPrime) { // save it! primes[numPrimes] = curPrime; numPrimes++; } } // End while // Print all the primes out. for (int i = 0; i <= numPrimes-1; i++) { System.out.println ("Prime: " + primes[i]); } return primes; } // end printPrime static Boolean isDivisable (int prime,int curPrime){ Boolean divisable = false; int remainder = curPrime % prime; if (remainder== 0){ divisable = true; } return divisable; } }
Then write the test code as follow:
import static org.junit.Assert.*; import org.junit.Before; import org.junit.Test; public class PrimeTest { private static Prime myTest = null; private static int[] myPrime = new int[100]; @Before public void setUp() throws Exception { myTest = new Prime(); myPrime[0] = 2; myPrime[1] = 3; myPrime[2] = 5; myPrime[3] = 7; myPrime[4] = 11; } @Test public void testPrintPrimes() { assertArrayEquals(myPrime,myTest.printPrimes(5)); } }
Test result: