《道生一,一生二,二生三,三生万物》出自老子的《道德经》第四十二章。主要讲述了一、二、三这几个数字,并不把一、二、三看作具体的事物和具体数量。它们只是表示“道”生万物从少到多,从简单到复杂的一个过程。(来自百度百科)
世界太奇妙了,cpu从0、1运算起,上层便可搭建操作系统、软件等。帮助了人们解决很多重复的、复杂的运算,那么我们返回来说,任何语言的计算都无法脱离0、1这两个数字,介于每次遇到位操作符我都要百度一次,用到的比较少所以不是很熟,另外记忆力始终不是很好,想想把自己的理解写出来,一来辅助自己的记忆,二来伙伴们可能也会有跟我同样记不住的。
先来理解几个java概念(以下内容均在java语言中描述):
bit(位):位运算符号指的就是这个bit运算
byte(字节) : 1byte 占 8bit
int(整数形) : 占4字节
大多数数据类型值范围参考下图:
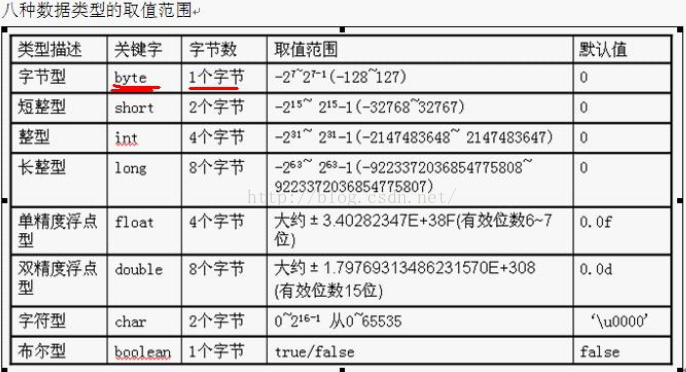
图片来源:http://blog.csdn.net/qq_27789551/article/details/52013596
在我们通常的印象中,大多数的单位转换比如 1斤=10两、1kg= 1000g 、1斤=500g、1km = 1000m、等等、但在bit byte int 方面我们还能这样来换算,我们理解1byte = 8bit、2byte= 16bit这种不能像1斤=10两、2斤=20两这种换算,因为斤量对应的类型是质量,而byte和bit是两个类型,1斤中的1表示的量也是值,但1byte、bit不是,1byte是指1个byte的类型的量,不是值,那么8bit也只能是8个bit的量,更明确的解释是1byte占8个bit,这个占如何在计算机中或者直观的用符号表示我还没有百度到,解释这一段是想说明的是比如:
byte b = 1时占用的是8个bit, byte b=2时占用的是16字节,这是错误的,无论b 为何值所占的bit均为8,一会我们再说什么时候占用的是16,什么时候占用的是32,那如何表示byte与bit的关系呢,字符串好像也行,数组好像也行,但在代码中是没有这样写的,我只是做一个形象的直观的方式
byte c = 1,对应的bit表现形式为
| bit位 | [7] | [6] | [5] | [4] | [3] | [2] | [1] | [0] | |
| 值 | x | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
或者是:byte c =1 = "x000 0001" bit 或者是 byte c = 1 = {x,0,0,0,0,0,0,1}
如果 byte = 2 则(接下来都简写为) byte c=2 = "x000 0010",byte = 3 则是 byte c =3 = "x000 0011",
为什么我把第7位值用x表示,实际在java中byte是有符号字节,这个符号就是第7位这个值,是用来表示正负的,现在重新来表示一下byte 1、2、3(十进制) 的二进制表现形式
正数:
3 = 0000 0011
2 = 0000 0010
1 = 0000 0001
0 = 0000 0000
我们试着向上找到最大的正值,0111 1111 ,换算成十进制则为127,换算方法详见http://blog.csdn.net/xy2204/article/details/50522075,
那么问题来了,把二进制加1,0111 1111 + 0000 0001,得到的结果是1000 0000,那么这个数对应byte的值是多少?
是128还是-1还是-128呢?我们使用java一段代码来验证我们的想法,看看结果是多少,如果不愿意打开eclipse 或者idea,有个在线工具可以玩玩,我觉得不错,http://www.dooccn.com/java/,在这里我们插入这行代码:
System.out.println(new Byte( (byte)(Byte.MAX_VALUE+1)) );
运行后结果是-128,我靠没搞错吧为什么是-128?我们再来看看刚才那个二进制串1000 0000,额。。。这个不应该是128吗,怎么就成了-128。。。,是,如果我们换一个语句执行
System.out.println(new Integer( (int)(Byte.MAX_VALUE+1)) ); 输出的结果居然就是128了,其中的原委在于我们设定的运算类型是以 byte运算还是以int 运算,如果以byte运算则运算的宽度为8,如果以int算宽度就是4个字节,每个字节8bit,就是32bit宽度,一会我们再说int。先说说这个-128,中国有句古语叫做化整为零,8bit太长了,我想把他变为4bit来理解,或者我定义一个类型叫smallbyte,占4个bit。我们来分解他加的过程
无符号二进制
二进制 十进制
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 10
1011 11
1100 12
1101 13
1110 14
1111 15
1 0000 0
上边这个是在无符号的情况下,4bit的二进制加1得到的十进制的最大值是15,最小值是0,当达到16的时候,二进制变成了5位,我们是以4位长度来计算的,那么这个1就是溢出的值,在计算长度只为4bit情况下,溢出的值会被另外处理,也就是说15+1使用4位来计算则结果是0,这个好像我们的钟表24点是终点,0点是起点,每当达到24小时时,天数增加,而时间变成了0这样周而复始,这个加一天是在天的范围内,不在几点的范围内,我们讨论时间的时候,天数加不加1我不管,反正我是24点结束就是0点,跟我们溢出的这个1是不是很像?他溢出了自然有另外的东西来表述他,但跟当前的4bit无关,4bit又变回了0,我们把这种首位相连的用钟表的图像来展示(虽然不够圆。。。)
0000 (0)
1111 (15) 0001 (1)
1110 (14) 0010 (2)
1101 (13) 0011 (3)
1100 (12) 0100 (4)
1011 (11) 0101 (5)
1010 (10) 0110 (6)
1001 (9) 0111 (7)
1000 (8)
看到这幅图我想起了常听到的一句古话,叫做物极必反,当达到最大值时下一个值就是最小值。当前上图所表示的都是正数,那负数怎么表示呢。。。java大神或者cpu大神就想啊,我把某一位标定为符号位来表示正负不就解决了吗,于是4位bit 变成了从右向左数第一位设定位符号位,为0时是正数,为1时是负数,此时,最大值正数则是{0111} = 7,我们看刚才的理论,最大值+1的下一个值一定是最小值,便是{1000},既然第一位是符号位那1不算,3个0结果是0啊,那是不是{1000}=-0呢,既然有负数那最小值一定不是0,当时懵就b了,这是怎么回事。。。,我们将上图旋转至最大最小值交界处向上,试了多种之后发现顺时针旋转180°时刚刚好最大值的左边是最大正数,如果我们设置最大值8为正数那么左右两边的个数会产生不平衡,我们根据最大正数{0 111}计算,很容易得到了最大正值是 7 ,那么最小负值是多少我们一元一次方程试着带入进来看看效果,
1000 (-x)
0111 (7) 1001 (-(x-1))
0110 (6) 1010 (-(x-2))
0101 (5) 1011 (-(x-3))
0100 (4) 1100 (-(x-4))
0011 (3) 1101 (-(x-5))
0010 (2) 1110 (-(x-6))
0001 (1) 1111 (-(x-7))
0000 (0)
根据规律,我们大概可以看出来x是多少,但实际的计算应该是0右边的数值一定是负一,那么-(x-7)得到的x就是8了,带入整个圈后,看起来就完美了
1000 (-8)
0111 (7) 1001 (-7)
0110 (6) 1010 (-6)
0101 (5) 1011 (-5)
0100 (4) 1100 (-4)
0011 (3) 1101 (-3)
0010 (2) 1110 (-2)
0001 (1) 1111 (-1)
0000 (0)
那么问题来了,看着好别扭,为什么不能左右对称,左边是{0001}(1)右边是{1001}(-1),而是{1111}为-1,看{1 111}的符号位为负数,我们知道整数的负数中最大值是-1,111是负值中最大的,那么把{1111}解释为-1就解释的通了,{1 000}为-8也就顺出来了。
为什么这么啰嗦的说了这么多,下面还要啰嗦,像我这个不常接触这个底层bit运算的人写了近10年的传统it业务代码了,居然对移位等操作并不熟悉(几乎用不到的),只是大概知道这么用,是脑海里残留的印象,所以此文针对的不是懂的人,懂的人不会找到这里来,还有一知半解的不知道怎么去消化这个东西的伙伴。其实上面所说的是我看到这些概念我脑海里所呈现出的分解方案,说了这么多实际有几个专有名词就替代了我解释bit有无符号的地方,另外来说我所理解的任何数学、科学都是建立在已有的世界事物做归类、抽象总结的结论,当我们不能理解这个抽象概念时就用自己的逻辑来试着分解、还原这种抽象,就像3*5,懂抽象概念乘法的人直接根据公式和小九九算出15、那不知道或者不能理解这个抽象的人掰了手指算就得到了15,殊途同归,接下来我们用抽象后的概念来进行记录。
原码、反码、补码、
下面连接是关于源码、反码、补码一些相关的链接,本文接下来会使用这些名词,不再赘述
http://blog.sina.com.cn/s/blog_65b11c760100hlsu.html
https://www.zhihu.com/question/20159860/answer/21113783
http://blog.csdn.net/liushuijinger/article/details/7429197
▷ https://www.cnblogs.com/zhangziqiu/archive/2011/03/30/ComputerCode.html
现在我们回到8位byte问题上来,根据4位bit理论结合抽象后的概念,解释8位的byte最大值和最小值
正数
0000 0001 b = (1)
0111 1111 b = (127)
负数(通用算法二进制转十进制的方法为先取反(运算符也取反),然后加1,根据运算符号位表示正负值
1111 1111 b = 取反0000 0000 +1= 0000 0001 (此时符号参与取反)转为十进制1=结果(初始运算符号为负) (-1)
1000 0000 b = 取反0111 1111+1=1000 0000(此时符号参与取反)转为十进制为128 = 结果(初始运算符号为负) (-128)
接下来我们主角int该登场了,在int正式出场前我们简单的小幅度的引用short出场
文章第一副图表示了 short占2个字节,对应的概念就是 short 1 = 0000 0000 0000 0001 b,也就是说一个short由两段byte 组成的16bit表示short。
int:占4字节(每个字节有8bit),也就是说 int 1 = 0000 0000 0000 0000 0000 0000 0000 0001 b
共32位或者32bit,以上的说法中我们只描述的是java中,但是在C#中 我们会看到不一样的类型,比如
Int32(java的int) ,Int16(java的short)
现在我们将int i = 2 的i的二进制显示为:
0000 0000 0000 0000 0000 0000 0000 0010
记得一些面试题中经常会有给一个数值2如何最快算出8,当我们对位操作不熟悉的时候通常的做法是2*4,那java或者cpu的某些指令处理最终给cpu的算法应该是2+2+2+2,像下面这样:
0000 0000 0000 0000 0000 0000 0000 0010
+
0000 0000 0000 0000 0000 0000 0000 0010 = 0000 0000 0000 0000 0000 0000 0000 0100
+
0000 0000 0000 0000 0000 0000 0000 0010 = 0000 0000 0000 0000 0000 0000 0000 0110
+
0000 0000 0000 0000 0000 0000 0000 0010 = 0000 0000 0000 0000 0000 0000 0000 1000
在处理2*4时会进行3次加法,我们来对比原值和新值之间的关系
2 = 0000 0000 0000 0000 0000 0000 0000 0010 b
8 = 0000 0000 0000 0000 0000 0000 0000 1000 b
呀,原来只是1的位置发生了变化,有没有什么算法不用这样加,直接将这个2的那个1移至8的那个1所在的位置呢?有!就是移位算法
左移( << ) : 操作符不变,用来将一个数的各二进制位全部左移若干位(通俗理解就是将带1的部分向左全部移动x位,0不动,最右边低位补0,移动几次补几个0)
2 << 2 得到的结果就是8,非常非常快不用加那么多次了
刚刚我们移动的是正数,如果是负数则移动为0的同样右边补0,例:-5 << 2结果是-20
-5 = 1111 1111 1111 1111 1111 1111 1111 1011
-20 = 1111 1111 1111 1111 1111 1111 1110 1100
右移( >> ) : 跟上边差不多就是方向是向右,操作符不变,负数情况下 左边高位补1,正数情况下补0,移动几次补几个0或1(下面例子蓝色表示补的)
正数
8 = 0000 0000 0000 0000 0000 0000 0000 1000 b
2 = 0000 0000 0000 0000 0000 0000 0000 0010 b
8 >> 2 得到的结果就是2,不用8/4了(减3次2那么麻烦了)
负数(高位补的蓝色的1)
-20 = 1111 1111 1111 1111 1111 1111 1110 1100
-5 = 1111 1111 1111 1111 1111 1111 1111 1011
▷现在试着练习一下,使用位移和加减法计算int最大值
无符号右移(>>>):直接在在高位补零,无符号位移是针对上面两个位移有符号的左移、右移所说的,例子如下:
正数 : 8>>>2 = 2,与有符号区别不大
8 = 0000 0000 0000 0000 0000 0000 0000 1000 b
2 = 0000 0000 0000 0000 0000 0000 0000 0010 b
负数: -8 >>>2 = 1073741822
-8 = 1111 1111 1111 1111 1111 1111 1111 1000
1073741822 = 0011 1111 1111 1111 1111 1111 1111 1110
就是说符号位也被补了,就变成了正数
无符号右移相关文章:https://jingyan.baidu.com/article/5552ef47e5618d518ffbc9db.html
位与( & ) :记作 a & b
计算 100 & 6
0000 0000 0000 0000 0000 0000 0110 0100 a = 100
&
0000 0000 0000 0000 0000 0000 0000 0110 b = 6
----------------------------------------------------
0000 0000 0000 0000 0000 0000 0000 0100 结果 = 4
位与( & ):运算方法是a同位有1,b同位有1时结果位才有是1,其他为0
记忆口诀:你有(1)我有(1)才算有,其他都是浮云(0),或者一 一得一,其余得零
ps:大多数文章所写的都是简写,如a & b = 1100100 & 110,需要右边对齐左边补0得到相同位数再进行计算比较好理解,像a & b = 1100100 & 110 = 01100100 & 0000 0110,以下同理
位或( | ):记作a | b
计算 33 | 25
0000 0000 0000 0000 0000 0000 0010 0011 a = 35
&
0000 0000 0000 0000 0000 0000 0000 1010 b = 10
----------------------------------------------------
0000 0000 0000 0000 0000 0000 0010 1011 结果 = 43
位或( | ):两个数只要有一个为1,那么结果就是1,否则就为0
记忆口诀:你的(1)就是我的,我的(1)还是我的,你我都没有才算没有(0),或者有奶(1)便是娘(1)(捂脸笑)
位非( ~ ):记作 ~ a
计算 ~66
0000 0000 0000 0000 0000 0000 0100 0010 a = 66
----------------------------------------------------
1111 1111 1111 1111 1111 1111 1011 1101 结果 = -67
位非( ~ ):原位为0的都变为1,原位为1的都变成零,就是取反的意思,符号位也取反,需要确定位数范围,byte 8位,short 16 位......
记忆口诀:天(1)对地(0),雨(0)对风(1)。大陆对长空,或者。。。
位异或( ^ ):记作a^b
计算 10 ^ 35
0000 0000 0000 0000 0000 0000 0000 1010 a = 10
^
0000 0000 0000 0000 0000 0000 0010 0011 b = 35
----------------------------------------------------
0000 0000 0000 0000 0000 0000 0010 1001 结果 = 41
位异或( ^ ):两个操作数的位中,相同则结果为0,不同则结果为1
记忆口诀:两数相减的绝对值
额。。。写完了。。。下篇会写相关的练习题,比如 & 0xFF是怎么回事。。。