1. 给你n个数,其中有且仅有一个数出现了奇数次,其余的数都出现了偶数次。用线性时间常数空间找出出现了奇数次的那一个数。(全部异或)
2. 给你n个数,其中有且仅有两个数出现了奇数次,其余的数都出现了偶数次。用线性时间常数空间找出出现了奇数次的那两个数。
3.给你一个数列,一次操作是指将某个数移到数列中别的位置上去,然后问最少要几次操作才能让数列变得有序。例如,数列7,1,3,2,6,5就只需要三次移动,把3移到2后面,把5移到6前面,再把7移到最后面即可。
ps:这题其实就是一个最长上升子序列问题。因为整个操作过程实质上可以等价地看作是,把要移动的数先全部取出来,再挨个放回适当的位置。这就要求取出要移动的数后,剩下的那些数本身是有序的。若希望要移动的数越少越好,那也就等于说是剩下的不动的数要越多越好。
4.给定一个图,你有一次机会将某条边的权值减半,用O(n^2)的时间求最短路。
ps: 这题的正确算法呢,其实也不难,预处理S到所有点的最短路,以及T到所有点的最短路,然后枚举每条边,可以直接求出将这条边减半后必须经过该边的最短路.这样,枚举得出的最小值就是我们所求的最短路。
5给定一个图,你有k次选一条边令其权值减半的机会,求最短路。
ps:其实这题有一个非常巧妙的O(n^2·k^2)的算法,真不知是谁想出来的:把原图分成k+1层,从0到k分别标号。上面的层到下面的层有很多单向边,每条边都和原图上的某条边相对应,跨越了几层权值就打几次对折,表示我“走了一条权值减过的边”。因此,你当前走在第几层,就表示你已经用掉了几次减半机会。在这个有O(nk)个顶点的图上做最短路,其结果就是我们所要求的。

6.在1到n中选取若干个数,要求如果选了x就不能选2x和3x,问共有多少种选择方案。例如,n=3时答案为5,这5种选法分别为{}, {1}, {2}, {3}, {2,3}。
ps:把数字1放在方阵最左下角,然后不断在一个数的右边填上它的两倍,在其上方填上它的三倍。问题就等价地转化为,在方阵中选取若干个格子使得任意两个不相邻,求有多少种选取方案。这是一个经典的带状态压缩的动态规划问题。另外,遇到尚未出现过的数(即除2和3以外的素数)就再开一张新的表,然后用乘法原理把它们各自对应的方案数乘起来就是了。例如当n=20时,最终答案就等于下面这7张表各自所对应的选取方案数的乘积。
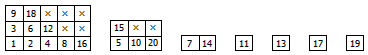
这题也许还有组合数学方法,但下面这个加强版估计就只能这样做了:如果再给定一些不能选的数,则又有多少种选择方案.