P1177 【模板】快速排序
不用说,连题目上都标了是一道模板,那今天就来对能用到的许多排序方式进行一个总结:
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法。(稳定不稳定最后再讲)

这是选择排序的思想:每一趟在n-i+1(i=1,2,3…,n-1)个记录中选取关键字最小的记录与第i个记录交换,并作为有序序列中的第i个记录。
例如:
待排序列: 43,65,4,23,6,98,2,65,7,79
第一趟: 2,65,4,23,6,98,43,65,7,79
第二趟: 2,4,65,23,6,98,43,65,7,79
第三趟: 2,4,6,23,65,98,43,65,7,79
第四趟: 2,4,6,7,43,65,98,65,23,79
第五趟: 2,4,6,7,23,65,98,65,43,79
第六趟: 2,4,6,7,23,43,98,65,65,79
第七趟: 2,4,6,7,23,43,65,98,65,79
第八趟: 2,4,6,7,23,43,65,65,98,79
第九趟: 2,4,6,7,23,43,65,65,79,98
贴个代码:
#include <iostream> using namespace std; void SelectSort(int a[], int n) //选择排序 { int mix, temp; for (int i = 0; i < n - 1; i++) //每次循环数组,找出最小的元素,放在前面,前面的即为排序好的 { mix = i; //假设最小元素的下标 for(int j=i+1;j<n;j++) //将上面假设的最小元素与数组比较,交换出最小的元素的下标 if (a[j] < a[mix]) mix = j; //若数组中真的有比假设的元素还小,就交换 if (i != mix) { temp = a[i]; a[i] = a[mix]; a[mix] = temp; } } } int main() { int a[10] = {43, 65, 4, 23, 6, 98, 2, 65, 7, 79}; SelectSort(a, 10); for (int i = 0; i < 10; i++) cout << a[i] << " "; cout << endl; return 0; }
很明显,我们用到了两个嵌套的循环,所以时间复杂度就是o(n^2)的
然鹅。。。。正常人都会觉得这算法太慢了吧!!!!!!
所以我们来讲个好一点的;
冒泡排序(也是我比较喜欢的一种)
具体思路是什么呢:
冒泡排序的基本思想为:
一趟冒泡排序的过程为:首先将第一个记录的关键字和第二个记录的关键字进行比较,若为逆序,则将两个记录交换之,然后比较第二个记录的关键字和第三个记录的关键字,依次类推,直至第n-1个记录和第n个记录的关键字进行过比较为止;
在冒泡排序的过程中,关键字较小的记录好比肥宅快乐水(雾)的气泡逐趟向上漂浮,而关键字较大的记录好比石头往下沉,每一趟有一块“最大”的石头沉到水底。
还是上面那个数
待排序列:43, 65, 4, 23, 6, 98, 2, 65, 7, 79
第一趟: 43, 4,23,6,65,2,65,7,79,98
第二趟: 4,23,6,43,2,65,7,65,79,98
第三趟: 4,6,23,2,43,7,65,65,79,98
第四趟: 4,6,2,23,7,43,65,65,79,98
第五趟: 4,2,6,7,23,43,65,65,79,98
第六趟: 2,4,6,7,23,43,65,65,79,98
冒泡排序的时间复杂度为:O(n^2),空间复杂度为O(1)
冒泡排序是稳定的;
好吧其实这俩货时间复杂度是一样的,但是我还是喜欢用冒泡QAQ
贴一下代码吧
#include <iostream> #include <algorithm> using namespace std; void bubleSort(int a[], int n) //冒泡排序 { //运用两个for循环,每次取出一个元素跟数组的其它元素比较,将最大的元素排到最后 for (int i = 0; i < n - 1; i++) { //外循环一次,就排好一个数,并放在后面,所以比较前面n-i-1个元素即可 for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a[j],a[j+1]);//swap其实和之前那个temp的作用是一样的,就是交换一下数字而已 } } } } int main() { int a[10] = {43, 65, 4, 23, 6, 98, 2, 65, 7, 79}; bubleSort(a, 10); for (int i = 0; i < 10; i++) cout << a[i] << " "; cout << endl; return 0; }
冒泡排序其实还有一个挺重要的用处,就是找一堆数里头的最大数和最小数,其实就是用的冒泡的方法
for(int i=1;i<=n;i++) { if(a[i]>Max) Max=a[i]; }
还有一个很重要的排序方式
快速排序
一听就很快啊有没有(雾)
快速排序的思想是找一个基准数,比基准数小的扔到左边去,大的扔到右边去(升序排列时)
听起来挺简单的吧,,,代码实现可能有一点点复杂,慢慢看
代码如下
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> using namespace std; int findPos(int a[], int low, int high) { //将小于t的元素赶到t的左边,大于t的元素赶到t的右边 int t = a[low]; while (low < high) { while (low < high && a[high] >= t) high--; a[low] = a[high]; while (low < high && a[low] <= t) low++; a[high] = a[low]; } a[low] = t; //返回此时t在数组中的位置 return low; } //在数组中找一个元素,对于大于该元素和小于该元素的两个数组进行再排序, //再对两个数组分为4个数组,再排序,直到最后每组只剩下一个元素为止 void quickSort(int a[], int low, int high) //快速排序 { if (low > high) return; int pos = findPos(a, low, high); quickSort(a, low, pos - 1); quickSort(a, pos + 1, high); } int main() { int, n, a[100000]; scanf("%d", &n); for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); quickSort(a, 1, sizeof(a)); for (int i = 0; i < 10; i++) cout << a[i] << " "; cout << endl; return 0; }
我们再来看看归并排序这个东西
归并排序(最不常用但是是实打实的快的算法)
将两个的有序数列合并成一个有序数列,我们称之为"归并"。
归并排序(Merge Sort)就是利用归并思想对数列进行排序。根据具体的实现,归并排序包括"从上往下"和"从下往上"2种方式。
基本思想:先将整个数组分成两个部分,分别将两个部分排好序,然后将两个排好序的数组O(n)合并成一个数组。
我们将问题分为两个阶段:分、治
分
对于每个长度> 1的区间,拆成两个[l, mid]区间
和[mid + 1, r]区间
直接递归下去

这样的话就可以一直递归直到只剩下一个数的时候,就分完了
治
我们认为在处理区间[l,r]时,已经有[l,mid]和[mid+1,r]内分别有序,这一次的操作就是合并两个有序序列,成为一个新的长有序序列。
用两个指针分别指向左右分别走到哪了即可
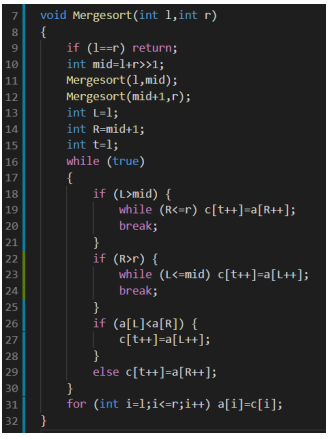
举一个例子吧,比如我们要合并这两个数组(模拟一下合并过程)
135
246
显然你肯定不能把246直接接到135后面对吧,这个时候我们建两个指针S1=1和S2=1(我的习惯是下标从1开始)
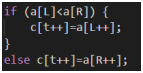
然后干这样一件事先比较a[s1]和b[s2]的大小,这里1更小一点,
所以
c[i]=b[s2];
S2++;
这里其实就是用两个指针分别从要合并的两个数组的头元素指起,如果元素被合并,那么就指针++,直到两个数组的指针都指完为止,就是这一块
算法的时间复杂度就是O(nlogN)
然后再看看堆排()
堆排吧,其实就是利用一个大根堆或者是小根堆来对一组数据进行合并和动态维护其顺序。
其代码本身并没有与堆的板子有太多差别,而是完全按照加入元素弹出元素那些函数来维护的,改一改就能交啦
自己黈自己(QWQ还是gh神仙给我纠正手写堆)
#include <iostream> #include <queue> #include <algorithm> #include <cstdio> using namespace std; int n, a, b, Heap[1000001], cnt = 0; inline void add(int x) { Heap[++cnt] = x; int now = cnt; while (now!=1) { if (Heap[now] < Heap[now >> 1]) swap(Heap[now], Heap[now >> 1]),now>>=1; else break; } } inline void pop() { printf("%d ", Heap[1]); Heap[1] = Heap[cnt--]; int root = 1; while (root << 1 <= cnt) { int son; if ((root << 1) + 1 > cnt || Heap[root << 1] < Heap[(root << 1) + 1]) { son = root << 1; } else son = (root << 1) + 1; if (Heap[son] > Heap[root]) break; swap(Heap[root], Heap[son]); root = son; } } int main() { scanf("%d", &n); for (int i = 1; i <= n; ++i) { scanf("%d", &b); add(b); } while(n) { pop(); n--; } return 0; }
值得注意的是,如果把一整个堆按照下标顺序输出去,往往是无序的
原因是这个:
堆是一个完全二叉树,所以所谓大小关系仅仅是一个树根和他的两个智障儿子的关系,而不是说按顺序输出一定是有序数列,
堆排序能完成排序,其实是依靠每一次都弹出堆顶元素,然后进行动态维护,所以最终输出的数列是一个有序数列。
上面是堆排,下面是快排,由此可见堆排的确是很快的

最后一个(超级无敌变态的做法)
c++自带STL
其实就是sort函数
头文件是#include <algorithm>
Sort函数有三个参数:
其实还是挺简单的吧。。。。。。。
主要是排序能够练习对于数组的运用,这是培养思维和能力的好方法,至于考场上嘛,,,,,,还是sort好啊(雾
最后,我们贴一下AC代码
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> using namespace std; int findPos(int a[], int low, int high) { //将小于t的元素赶到t的左边,大于t的元素赶到t的右边 int t = a[low]; while (low < high) { while (low < high && a[high] >= t) high--; a[low] = a[high]; while (low < high && a[low] <= t) low++; a[high] = a[low]; } a[low] = t; //返回此时t在数组中的位置 return low; } //在数组中找一个元素,对于大于该元素和小于该元素的两个数组进行再排序, //再对两个数组分为4个数组,再排序,直到最后每组只剩下一个元素为止 void quickSort(int a[], int low, int high) //快速排序 { if (low > high) return; int pos = findPos(a, low, high); quickSort(a, low, pos - 1); quickSort(a, pos + 1, high); } int main() { int n, a[100000]; scanf("%d", &n); for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); quickSort(a, 1, n); for (int i = 1; i <= n; i++) cout << a[i] << " "; cout << endl; return 0; }