树 先序遍历 中序遍历 后序遍历

 写之前先看作用：

先序遍历：在第一次遍历到节点时就执行操作，一般只是想遍历执行操作（或输出结果）可选用先序遍历；

中序遍历：对于二分搜索树，中序遍历的操作顺序（或输出结果顺序）是符合从小到大（或从大到小）顺序的，故要遍历输出排序好的结果需要使用中序遍历

后序遍历：后续遍历的特点是执行操作时，肯定已经遍历过该节点的左右子节点，故适用于要进行破坏性操作的情况，比如删除所有节点

先序：中 左 右的顺序（先访问根节点，先序遍历左子树，先序遍历右子树）

中序：左 中 右的顺序

后序：左 右 中的顺序

遍历过程相同，只是访问各个节点的时机不同

先序遍历

 递归实现：

    public static void preOrderRecur(TreeNode treeNode)
    {
        if (treeNode==null)
        {
            return;
        }
        System.out.println(treeNode.val);
        preOrderRecur(treeNode.left);
        preOrderRecur(treeNode.right);
    }

够简单，需要注意终止条件。否则会空指针异常。

非递归实现（自己维护一个栈）：

public static void preOrder(TreeNode treeNode)
    {
        if(treeNode==null)
        {
            return;
        }
        Stack<TreeNode> stack = new Stack<TreeNode>();//注意泛型
        stack.push(treeNode);
        while (stack.size()!=0)
        {
            treeNode=stack.pop();
            System.out.println(treeNode.val + " ");
            if(treeNode.right!=null)//注意不为null的条件，否则出栈会空指针
            {
                stack.push(treeNode.right);//由于先处理左子树，后处理右子树，所以压栈顺序反过来就行
            }
            if(treeNode.left!=null)
            {
                stack.push(treeNode.left);
            }

        }
    }

这个迭代写的有点像递归了。。。

中序遍历

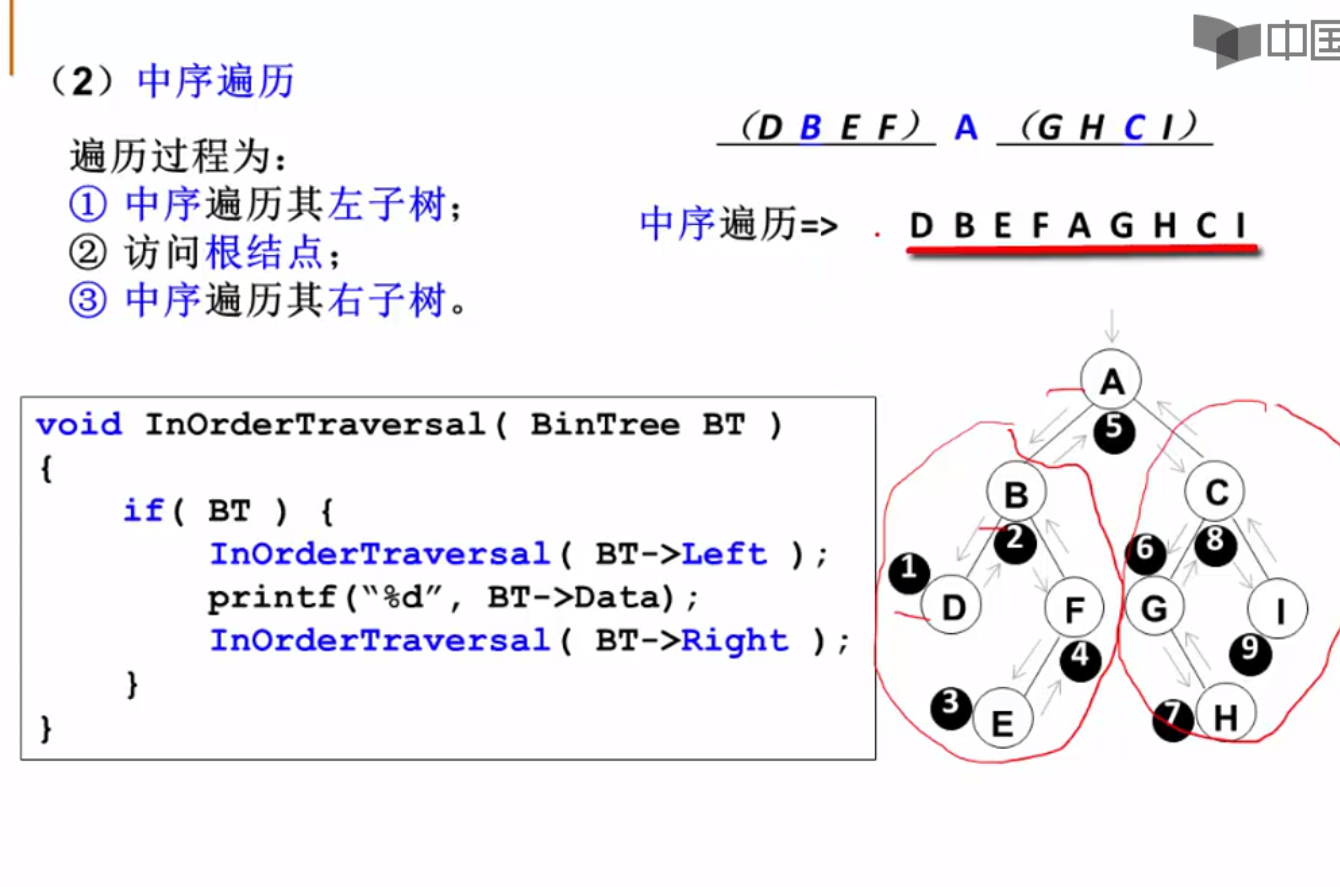
递归写法，真的爽，不用考虑具体的压栈过程，关注什么时候结束和递归逻辑就行

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        parse(root,list); 
        return list;       
    }

    public void parse(TreeNode root,List<Integer> list)
    {
        if(root==null)
        {
            return;
        }
        parse(root.left,list);
        list.add(root.val);
        parse(root.right,list);
    }
}

非递归写法：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack=new Stack<>();
        List<Integer> list=new ArrayList<>();
        while(stack.size()>0||root!=null)
        {
            while(root!=null)//处理root节点，去往最左侧，出循环后栈顶为优先级最高节点
            {
                stack.push(root);
                root=root.left;
            }
            TreeNode outNode=stack.pop();//到这里保证左侧已经没有东西了,outnode代表目前全树优先级最高的节点
            list.add(outNode.val);//处理“中”
            if(outNode.right!=null)//处理“右”，这一步加上去往最左能保证右子树被处理完
            {
                root=outNode.right;
            }
        } 
        return list;
    }   
}

• root是要处理的节点，当root不为null时，还没有找到最高优先级的节点，当root为null时，最高优先级节点在栈顶，且这个最高优先级节点的父亲在栈的第二位
• 处理最高优先级节点的办法是，弹出栈，输出最高优先级节点，处理右子树（即把root设置为其右孩子）
• 还是有点绕的。。。

后序遍历

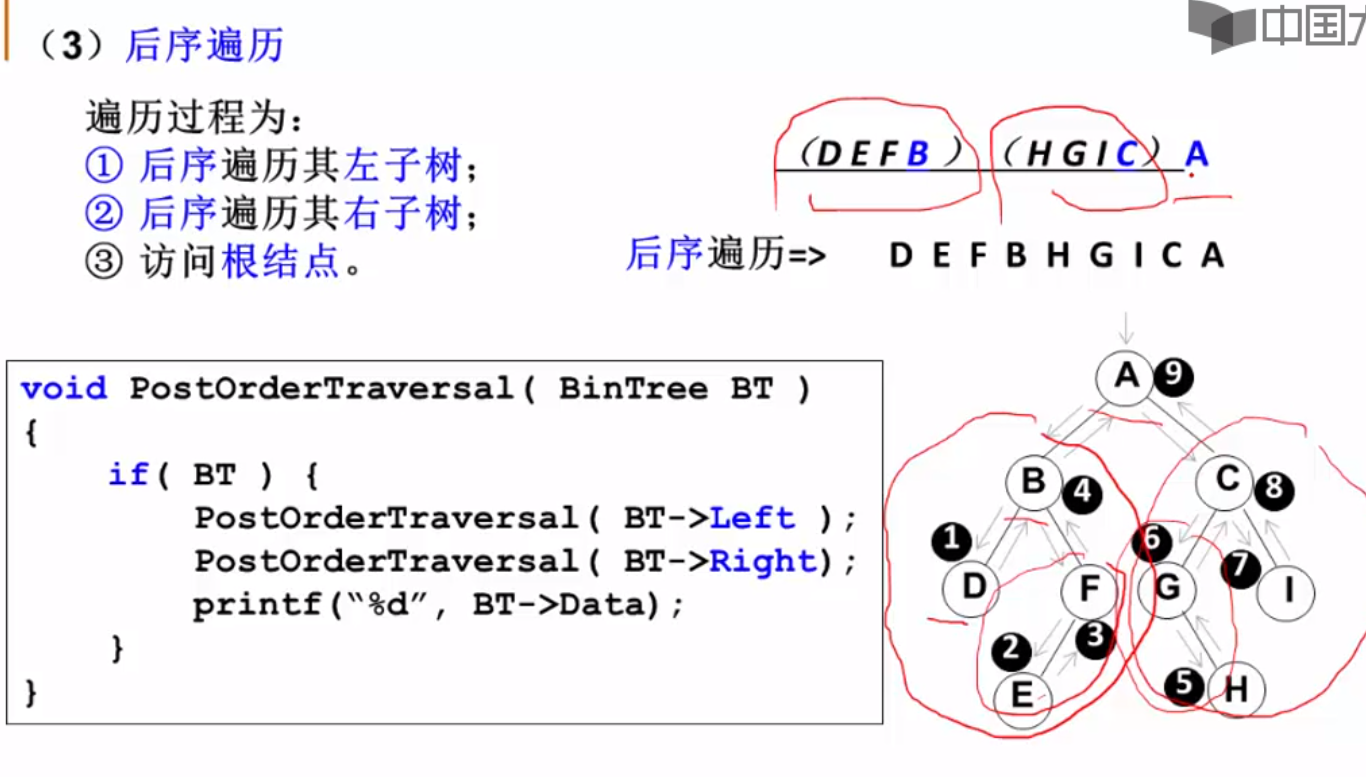
递归写法，差不多

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        postOrder(root,list);
        return list;
    }

    public void postOrder(TreeNode root,List<Integer> list)
    {
        if(root==null)
        {return;}
        postOrder(root.left,list);
        postOrder(root.right,list);
        list.add(root.val);
    }
}

非递归写法有两种

第一种：双栈法，前序遍历不是中左右，改变一下压栈顺序就成了中右左，倒序过来就是左右中。

倒序使用第二个栈就能实现，记录下来出栈的节点就可以

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        if(root==null)
        {return list;}
        Stack<TreeNode> stackReverse=new Stack<TreeNode>();
        Stack<TreeNode> stackResult=new Stack<TreeNode>();
        stackReverse.push(root);
        while(stackReverse.size()>0)
        {
            root=stackReverse.pop();
            stackResult.add(root);
            if(root.left!=null)
            {stackReverse.push(root.left);}
            if(root.right!=null)
            {stackReverse.push(root.right);}
        }
        while(stackResult.size()>0)
        {
            list.add(stackResult.pop().val);
        }
        return list;
    }
}

 第二种，硬写呗

和中序遍历有点像，先要找优先级最高的节点root，往左探

当root为null时，cur=stack.pop，但是此时优先级更高的不是cur而是cur.right

所以加入cur.right不为null，肯定要先处理右侧节点，cur要先放回栈

为了到时右侧节点被处理完了，cur再出栈时能知道，所以加了一个pre（因为cur.right处理完肯定下一个就是cur）

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        if(root==null)
        {return list;}
        Stack<TreeNode> stack=new Stack<TreeNode>();
        TreeNode pre=null;
        while(stack.size()>0||root!=null)
        {
            while(root!=null)
            {
                stack.push(root);
                root=root.left;
            }
            TreeNode cur=stack.pop();
            if(cur.right==null||pre==cur.right)
            {
                list.add(cur.val);
                pre=cur;
            }
            else
            {
                stack.push(cur);
                root=cur.right;
            }
        }
        return list;
    }
}