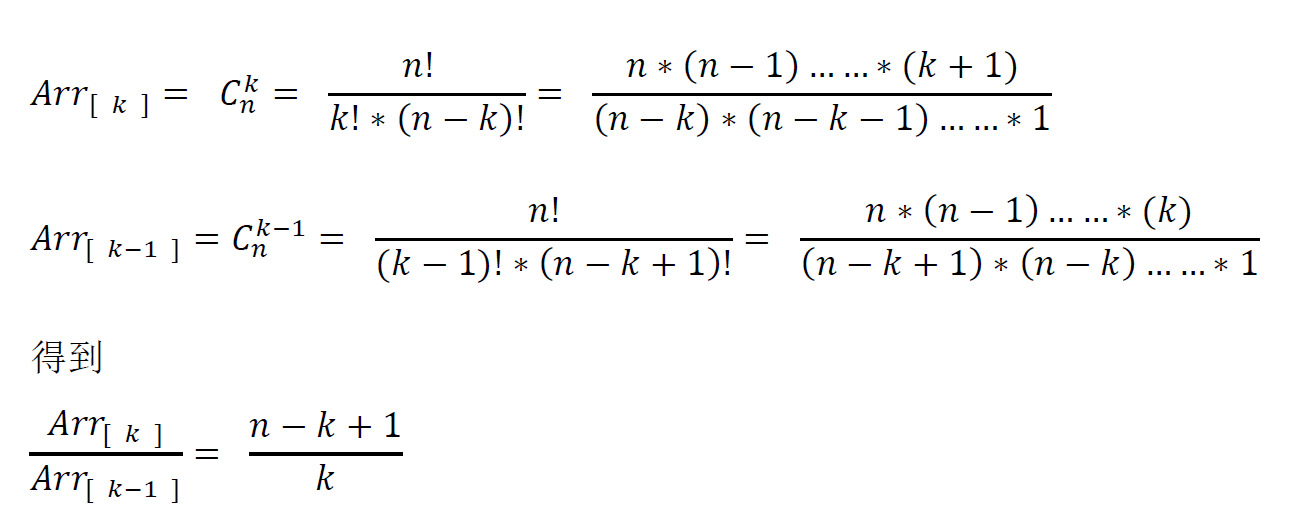Given an index k, return the kth row of the Pascal's triangle.
For example, given k = 3,
Return [1,3,3,1].
Note:
Could you optimize your algorithm to use only O(k) extra space?
- 要求空间复杂度为 O(n )
- 和上题不同,此题是从0开始,和数组下标一致
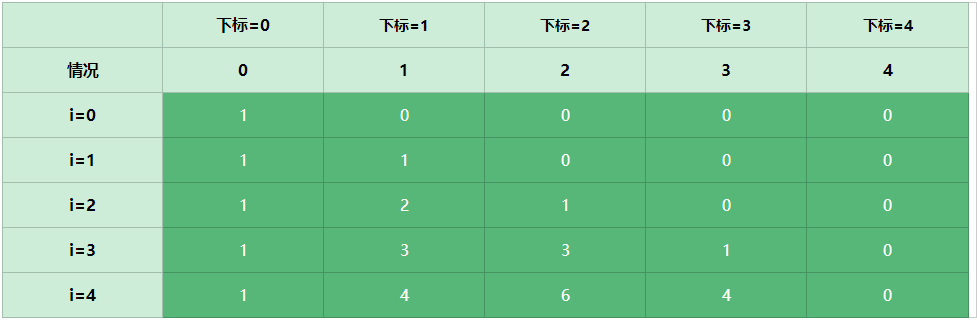
关于杨辉三角的规律

Method1 :通过一维数组来模拟杨辉三角逐渐变换的情况
class Solution { public: vector<int> getRow(int numRows) { vector<int>result(numRows+1,0); result[0] = 1; for (int i=1; i <= numRows; i++) { for (int j=i; j >= 1 ; j--) { result[j] += result[j-1]; } } return result; } };
数学公式
class Solution {
public:
vector<int> getRow(int numRows) {
vector<int>result(numRows+1,0);
result[0] = result[numRows] = 1;
for (int i=1; i < (numRows+2)/2 ; i++)
{
result[i] = result[numRows-i] = result[i-1] * (numRows - i + 1) /i;
}
return result;
}
};
公式是 result[i] = result[i-1] * (numrows - i + 1 ) / i
证明过程如下;
根据杨辉三角的规律,注意 杨辉三角中第 n 行 第 k 个数字 对对应于数组中的 第 n -1 行 第 k -1 个数字 ,题目中要求输入的是数组角标