一:区间选点
题目:
给定N个闭区间[ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数N,表示区间数。
接下来N行,每行包含两个整数ai,biai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需的点的最小数量。
数据范围
1≤N≤1051≤N≤105,
−109≤ai≤bi≤109−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2
解析:
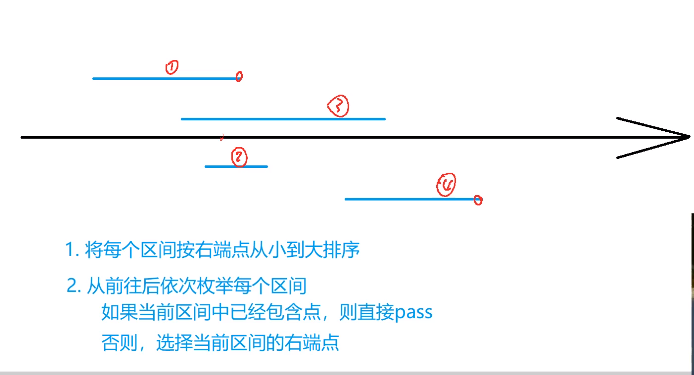
代码:

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N = 1e5+10; 5 6 struct Range{ 7 int l, r; 8 bool operator < (const Range& t){ 9 return r < t.r; 10 } 11 }range[N]; 12 13 int main(){ 14 int n;cin >> n; 15 for(int i = 0;i < n;++i) cin >> range[i].l >> range[i].r; 16 sort(range, range+n); 17 int ans = 0; 18 int last = -0x3f3f3f3f; 19 for(int i = 0;i < n;++i) 20 if(range[i].l > last){ 21 ++ans; 22 last = range[i].r; 23 } 24 cout << ans << endl; 25 return 0; 26 }
二:最大不相交区间数量
题目:
给定N个闭区间[ai,bi],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。
输出可选取区间的最大数量。
输入格式
第一行包含整数N,表示区间数。
接下来N行,每行包含两个整数ai,biai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示可选取区间的最大数量。
数据范围
1≤N≤1051≤N≤105,
−109≤ai≤bi≤109−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2分析: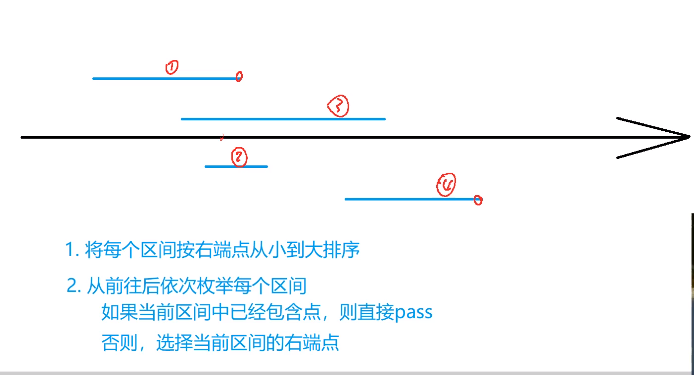
代码:

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N = 1e5+10; 5 6 struct Range{ 7 int l, r; 8 bool operator < (const Range& t){ 9 return r < t.r; 10 } 11 }range[N]; 12 13 int main(){ 14 int n;cin >> n; 15 for(int i = 0;i < n;++i) cin >> range[i].l >> range[i].r; 16 sort(range, range+n); 17 int ans = 0; 18 int last = -0x3f3f3f3f; 19 for(int i = 0;i < n;++i) 20 if(range[i].l > last){ 21 ++ans; 22 last = range[i].r; 23 } 24 cout << ans << endl; 25 return 0; 26 }
例题:
https://leetcode-cn.com/problems/maximum-length-of-pair-chain/
代码:

1 class Solution { 2 public: 3 int findLongestChain(vector<vector<int>>& pairs) { 4 //方法一,动态规划(最长上升子序列思路) 5 /* 6 sort(pairs.begin(), pairs.end());//这里排序是因为保证以当前数对为结尾的最长数对只会产生在当前数对的左面 7 vector<int> dp(pairs.size()+10, 1);//从起点到当前数对的最长上升个数 8 int ans = 0; 9 for(int i = 1;i < pairs.size();++i){ 10 for(int j = 0;j < i;++j){ 11 if(pairs[j][1] < pairs[i][0]) 12 dp[i] = max(dp[i], dp[j] + 1); 13 } 14 ans = max(ans, dp[i]); 15 } 16 return ans; 17 */ 18 //方法二,贪心(区间贪心问题) 19 //排序为了找到小于当前数对左端点的第一个数 20 sort(pairs.begin(), pairs.end(), [](const auto& a, const auto& b){ 21 return a[1] < b[1]; 22 }); 23 int ans = 0; 24 int cur = INT_MIN;//cur是当前上升数对的右端点 25 for(auto t : pairs){ 26 if(t[0] > cur){ 27 ++ans; 28 cur = t[1]; 29 } 30 } 31 return ans; 32 } 33 };
三:区间分组
题目:
给定N个闭区间[ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数N,表示区间数。
接下来N行,每行包含两个整数ai,biai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示最小组数。
数据范围
1≤N≤1051≤N≤105,
−109≤ai≤bi≤109−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2
分析:

代码:

1 #include <iostream> 2 #include <algorithm> 3 #include <queue> 4 using namespace std; 5 6 const int N = 1e5+10; 7 8 struct Interval{ 9 int l, r; 10 bool operator< (const Interval& t){ 11 return l < t.l; 12 } 13 }inter[N]; 14 15 int main(){ 16 int n;cin >> n; 17 for(int i = 1;i <= n;++i) cin >> inter[i].l >> inter[i].r ; 18 19 sort(inter+1, inter+n+1);//按照左端点排序 20 21 priority_queue<int, vector<int>, greater<int>> pq;//存储每一组的max_r 22 for(int i = 1;i <= n;++i){ 23 auto t = inter[i]; 24 if(pq.empty() || t.l <= pq.top()) 25 pq.push(t.r); 26 else{ 27 pq.pop(); 28 pq.push(t.r); 29 } 30 } 31 cout << pq.size() << endl; 32 return 0; 33 }
四:区间覆盖
题目:
给定N个闭区间[ai,bi]以及一个线段区间[s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出-1。
输入格式
第一行包含两个整数s和t,表示给定线段区间的两个端点。
第二行包含整数N,表示给定区间数。
接下来N行,每行包含两个整数ai,biai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需最少区间数。
如果无解,则输出-1。
数据范围
1≤N≤1051≤N≤105,
−109≤ai≤bi≤109−109≤ai≤bi≤109,
−109≤s≤t≤109−109≤s≤t≤109
输入样例:
1 5
3
-1 3
2 4
3 5
输出样例:
2
分析:

代码:

1 #include <iostream> 2 #include <algorithm> 3 using namespace std; 4 5 const int N = 1e5+10; 6 7 struct Interval{ 8 int l, r; 9 bool operator< (const Interval& t){ 10 return l < t.l; 11 } 12 }inter[N]; 13 14 int main(){ 15 int st, ed;cin >> st >> ed; 16 int n;cin >> n; 17 for(int i = 1;i <= n;++i) cin >> inter[i].l >> inter[i].r; 18 19 sort(inter+1, inter+n+1); 20 21 int ans = 0; 22 for(int i = 1;i <= n;++i){ 23 int j = i; 24 int r = -0x3f3f3f3f; 25 //在所有 l <= st 的区间中找到最靠的 26 while(j <= n && inter[j].l <= st){ 27 r = max(r, inter[j].r); 28 ++j; 29 } 30 //如果最靠右的小于st无解 31 if(r < st){ 32 cout << "-1" << endl; 33 return 0; 34 } 35 36 ++ans; 37 38 if(r >= ed){ 39 cout << ans << endl; 40 return 0; 41 } 42 43 st = r; 44 i = j - 1; 45 } 46 cout << -1 << endl; 47 return 0; 48 }
end
