一、基本思想
1)访问指定的起始顶点v;
2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
二、图的存储结构
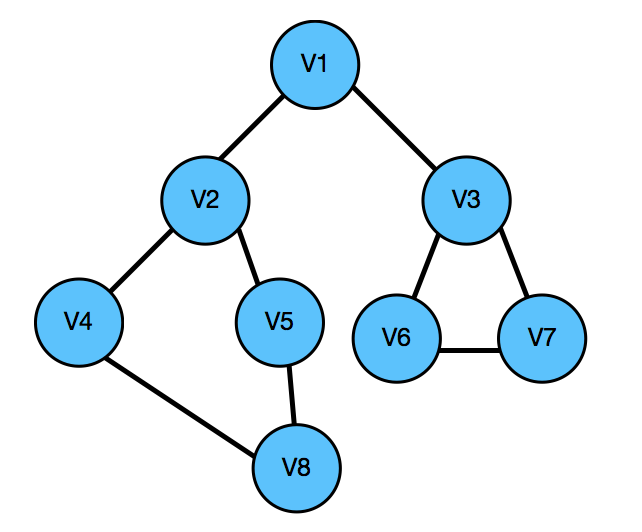
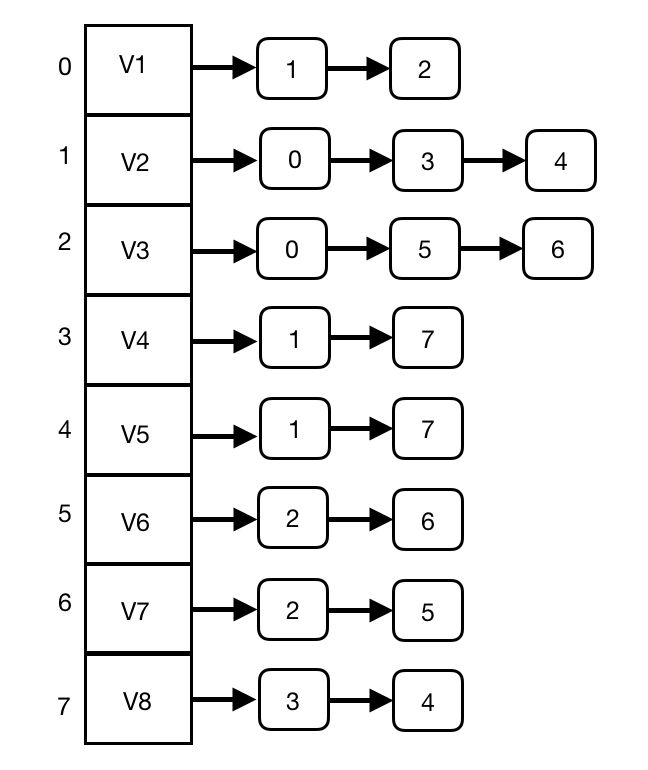
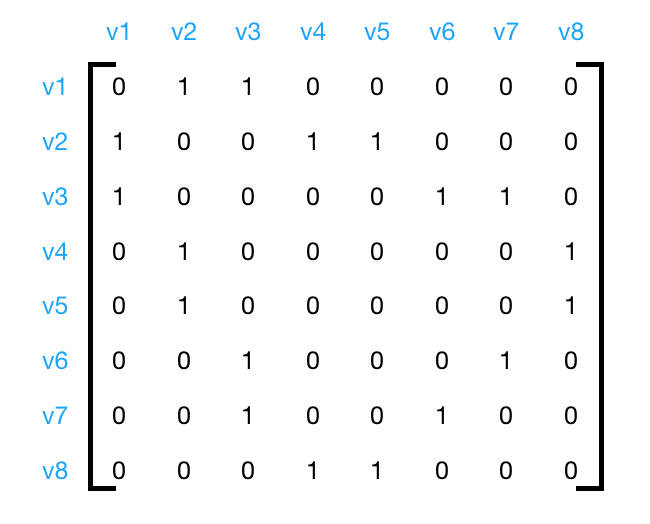
示例图 图的邻接表存储方式 图的邻接矩阵存储方式
三、实现方式
1、邻接表
<?php /** * 图的深度优先遍历 * 图的存储结构--邻接表 */ class Node{ public $value = null; public $next = [];//存储下一个节点位置的数组 public function __construct($value = null){ $this->value = $value; } } class Graph { // 记录节点是否已被遍历 public $visited = []; // 图的邻接表数组 public $graph = []; /** * 为顶点添加邻接点 * @param $vertex 顶点v * @param $adjvex 顶点v的邻接点 */ public function addVertex($vertex, $adjvex) { $this->graph[$vertex][] = $adjvex; } // 将邻接表数组转为邻接链表 public function createGraph() { $vertices = array_keys($this->graph); $result = []; foreach ($vertices as $vertex) { $result[$vertex] = new Node($vertex); } foreach ($this->graph as $vertex => $adjvex) { foreach ($adjvex as $v) { if (isset($result[$v]) && is_object($result[$v])) { $result[$vertex]->next[] = $result[$v]; } } } return $result; } /** * 递归 * @param $v 传入的是第一个需要访问的顶点 */ public function dfs($v) { // 置已访问标记 $this->visited[$v] = 1; // 输出被访问顶点 echo $v . PHP_EOL; // print_r($this->graph[$v]);die; for ($i = 0; $i < count($this->graph[$v]); $i++) { if ($this->visited[$this->graph[$v][$i]] == 0) { $this->dfs($this->graph[$v][$i]); } else { continue; } } } /** * 非递归 * @param $v 传入的是第一个需要访问的顶点 */ public function deepFirstSearch($v) { // 初始化节点遍历标记 $vertices = array_keys($this->graph); foreach ($vertices as $vertex) { $this->visited[$vertex] = 0; } $stack[] = $v; while (!empty($stack)) { $current = array_pop($stack); if ($this->visited[$current->value] == 0) { echo $current->value . PHP_EOL; $this->visited[$current->value] = 1; } for ($i = count($current->next) - 1; $i >= 0; $i--) { if ($this->visited[$current->next[$i]->value] == 0) { $stack[] = $current->next[$i]; } } } } } // 测试 $vertices = ['v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v7', 'v8']; $g = new Graph(); $g->addVertex('v1', 'v2'); $g->addVertex('v1', 'v3'); $g->addVertex('v2', 'v1'); $g->addVertex('v2', 'v4'); $g->addVertex('v2', 'v5'); $g->addVertex('v3', 'v1'); $g->addVertex('v3', 'v6'); $g->addVertex('v3', 'v7'); $g->addVertex('v4', 'v2'); $g->addVertex('v4', 'v8'); $g->addVertex('v5', 'v2'); $g->addVertex('v5', 'v8'); $g->addVertex('v6', 'v3'); $g->addVertex('v6', 'v7'); $g->addVertex('v7', 'v3'); $g->addVertex('v7', 'v6'); $g->addVertex('v8', 'v4'); $g->addVertex('v8', 'v5'); //print_r($g->graph); // 递归 $g->dfs($vertices[0]); // 非递归 $firstVertex = current($g->createGraph()); $g->deepFirstSearch($firstVertex);
2、邻接矩阵
<?php /** * 图的深度优先遍历 * 图的存储结构--邻接矩阵 */ class Graph { // 存储节点信息 public $vertices; // 存储边信息 public $arcs; // 图的节点数 public $vexnum; // 记录节点是否已被遍历 public $visited = []; // 初始化 public function __construct($vertices) { $this->vertices = $vertices; $this->vexnum = count($this->vertices); for ($i = 0; $i < $this->vexnum; $i++) { for ($j = 0; $j < $this->vexnum; $j++) { $this->arcs[$i][$j] = 0; } } } // 两个顶点间添加边(无向图) public function addEdge($a, $b) { if ($a == $b) { // 边的头尾不能为同一节点 return; } $this->arcs[$a][$b] = 1; $this->arcs[$b][$a] = 1; } // 从第i个节点开始深度优先遍历 public function traverse($i) { // 标记第i个节点已遍历 $this->visited[$i] = 1; // 打印当前遍历的节点 echo $this->vertices[$i] . PHP_EOL; // 遍历邻接矩阵中第i个节点的直接联通关系 for ($j = 0; $j < $this->vexnum ; $j++) { // 目标节点与当前节点直接联通,并且该节点还没有被访问,递归 if ($this->arcs[$i][$j] == 1 && $this->visited[$j] == 0) { $this->traverse($j); } } } // 递归 public function dfs() { // 初始化节点遍历标记 for ($i = 0; $i < $this->vexnum; $i++) { $this->visited[$i] = 0; } // 从没有被遍历的节点开始深度遍历 for ($i = 0; $i < $this->vexnum; $i++) { if ($this->visited[$i] == 0) { // 若是连通图,只会执行一次 $this->traverse($i); } } } // 非递归 public function deepFirstSearch() { // 初始化节点遍历标记 for ($i = 0; $i < $this->vexnum; $i++) { $this->visited[$i] = 0; } $stack = []; for ($i = 0; $i < $this->vexnum; $i++) { if (!$this->visited[$i]) { $stack[] = $i; while (!empty($stack)) { // 出栈 $curr = array_pop($stack); // 如果该节点还没有被遍历,则遍历该节点并将子节点入栈 if ($this->visited[$curr] == 0) { echo $this->vertices[$curr] . PHP_EOL; $this->visited[$curr] = 1; // 没遍历的子节点入栈 for ($j = $this->vexnum - 1; $j >= 0; $j--) { if ($this->arcs[$curr][$j] == 1 && $this->visited[$j] == 0) { $stack[] = $j; } } } } } } } } // 测试 $vertices = ['v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v7', 'v8']; $graph = new Graph($vertices); $graph->addEdge(0, 1); // v1 v2 $graph->addEdge(0, 2); // v1 v3 $graph->addEdge(1, 3); // v2 v4 $graph->addEdge(1, 4); // v2 v5 $graph->addEdge(2, 5); // v3 v6 $graph->addEdge(2, 6); // v3 v7 $graph->addEdge(4, 7); // v5 v8 $graph->addEdge(3, 7); // v4 v8 // 递归 $graph->dfs(); // 非递归 $graph->deepFirstSearch();