排序(不全以后补)
基数排序
原理:
https://www.jb51.net/article/129428.htm
package com.atguigu.sort;
import org.junit.Test;
import java.util.ArrayList;
import java.util.List;
/**
* @anthor shkstart
* @create 2020-08-16 15:03
*/
public class JSsort {
@Test
public void test(){
int[] array = {135,242,192,93,345,11,24,19};
radixSort(array);
}
public void radixSort(int[] array){
int max = array[0];
for (int i=0;i<array.length;i++){
//找到数组中的最大值
if(array[i]>max){
max = array[i];
}
}
int keysNum = 0;
//关键字的个数,我们使用个位、十位、百位...当做关键字,所以关键字的个数就是最大值的位数
while(max>0){
max /= 10;
keysNum++;
}
List<ArrayList<Integer>> buckets = new ArrayList<ArrayList<Integer>>();
for (int i=0;i<10;i++){
//每位可能的数字为0~9,所以设置10个桶
buckets.add(new ArrayList<Integer>());
//桶由ArrayList<Integer>构成
}
for (int i=0;i<keysNum;i++){
//由最次关键字开始,依次按照关键字进行分配
for (int j=0;j<array.length;j++){
//扫描所有数组元素,将元素分配到对应的桶中
//取出该元素对应第i+1位上的数字,比如258,现在要取出十位上的数字,258%100=58,58/10=5
int key =array[j]%(int)Math.pow(10, i+1)/(int)Math.pow(10, i);
buckets.get(key).add(array[j]);
//将该元素放入关键字为key的桶中
}
//分配完之后,将桶中的元素依次复制回数组
int counter = 0;
//元素计数器
for (int j=0;j<10;j++){
ArrayList<Integer> bucket =buckets.get(j);
//关键字为j的桶
while(bucket.size()>0){
array[counter++] = bucket.remove(0);
//将桶中的第一个元素复制到数组,并移除
}
}
System.out.print("第"+(i+1)+"轮排序:");
for (int n= 0;n < array.length;n++){
System.out.print(array[n]+ " ");
}
System.out.println();
}
}
}
快速排序
原理
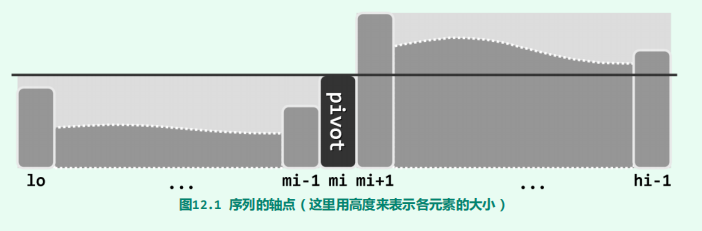

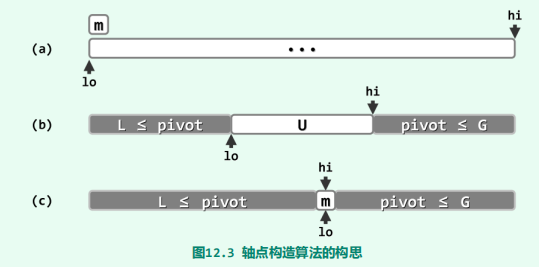
不妨取首元素m = S[lo]作为候选,将其从向量中取出并做备份,腾出的空闲单元便于其它元素的位置调整。然后如图(b)所示,不断试图移动lo和hi,使之相互靠拢。当然,整个移动过程中,需始终保证lo(hi)左侧(右侧)的元素均不大于(不小于)m。最后如图(c)所示,当lo与hi彼此重合时,只需将原备份的m回填至这一位置,则S[lo = hi]=m便成为一个名副其实的轴点
package com.atguigu.sort;
import org.junit.Test;
/**
* @anthor shkstart
* @create 2020-08-16 15:03
*/
public class Quicksort {
@Test
public void test() {
int[] array = {135,242,192,93,345,11,24,19};
this._elem = array;
this.quickSort(0,8);
for (int i = 0;i < 8;i++){
System.out.print(this._elem[i] + " ");
}
}
public int[] _elem = new int[8];
public void quickSort(int lo,int hi){
if (hi - lo < 2) return;
int mi = partition1(lo,hi - 1);
quickSort(lo,mi);
quickSort(mi+1,hi);
}
/**
* 子任务规模接近在这里却无法保证
* 若在最终有序向量中该候选元素的秩为r,则子向量的规模必为r和n - r - 1。
* 特别地,r = 0时子向量规模分别为0和n - 1左侧子向量为空,而右侧子向量与原向量几乎等长
*/
public int partition1(int lo,int hi){
swap(_elem[lo],_elem[(int) (lo + Math.random()*(100)%(hi - lo + 1))]);
int pivot = _elem[lo];
while (lo < hi){
while ((lo < hi) && (pivot <= _elem[hi])){
hi--;
}
_elem[lo] = _elem[hi];
while ((lo < hi) && (_elem[lo] <= pivot)){
lo++;
}
_elem[hi] = _elem[lo];
}
_elem[lo] = pivot;
return lo;
}
public void swap(int a,int b){
int c = a;
a = b;
b = c;
}
/**
* 将交替地将右(左)侧元素转移至左(右)侧,并最终恰好将轴点置于正中央的位置。
* 这就意味着,退化的输入向量能够始终被均衡的切分,如此反而转为最好情况,
*/
public int partition2(int lo,int hi){
swap(_elem[lo],_elem[(int) (lo + Math.random()*(100)%(hi - lo + 1))]);
int pivot = _elem[lo];
while (lo < hi){
while ((lo < hi)){
if (pivot < _elem[hi]){
hi--;
} else {
_elem[lo++] = _elem[hi];
break;
}
}
while ((lo < hi)){
if (_elem[lo] < pivot){
lo++;
} else {
_elem[hi--] = _elem[lo];
break;
}
}
}
_elem[lo] = pivot;
return lo;
}
}
实现
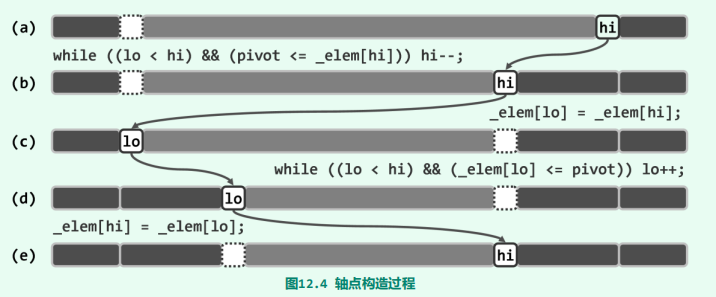

/**
* 子任务规模接近在这里却无法保证
* 若在最终有序向量中该候选元素的秩为r,则子向量的规模必为r和n - r - 1。
* 特别地,r = 0时子向量规模分别为0和n - 1左侧子向量为空,而右侧子向量与原向量几乎等长
*/
public int partition1(int lo,int hi){
swap(_elem[lo],_elem[(int) (lo + Math.random()*(100)%(hi - lo + 1))]);
int pivot = _elem[lo];
while (lo < hi){
while ((lo < hi) && (pivot <= _elem[hi])){
hi--;
}
_elem[lo] = _elem[hi];
while ((lo < hi) && (_elem[lo] <= pivot)){
lo++;
}
_elem[hi] = _elem[lo];
}
_elem[lo] = pivot;
return lo;
}
public void swap(int a,int b){
int c = a;
a = b;
b = c;
}
实例
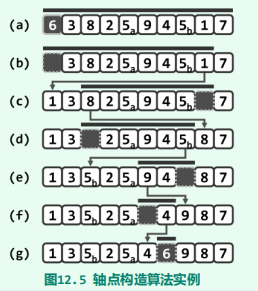
改进

考查所有(或几乎所有)元素均重复的退化情况。partition()算法的版本A对此类输入的处理完全等效于此前所举的最坏情况。事实上对于此类向量,主循环内部前一子循环的条件中“pivot <= elem[hi]”形同虚设,故该子循环将持续执行,直至“lo < hi”不再满足
/**
* 将交替地将右(左)侧元素转移至左(右)侧,并最终恰好将轴点置于正中央的位置。
* 这就意味着,退化的输入向量能够始终被均衡的切分,如此反而转为最好情况,
*/
public int partition2(int lo,int hi){
swap(_elem[lo],_elem[(int) (lo + Math.random()*(100)%(hi - lo + 1))]);
int pivot = _elem[lo];
while (lo < hi){
while ((lo < hi)){
if (pivot < _elem[hi]){
hi--;
} else {
_elem[lo++] = _elem[hi];
break;
}
}
while ((lo < hi)){
if (_elem[lo] < pivot){
lo++;
} else {
_elem[hi--] = _elem[lo];
break;
}
}
}
_elem[lo] = pivot;
return lo;
}
选取与中位数
众数
- 原理




- 实现
package com.atguigu.sort;
import org.junit.Test;
/**
* @anthor shkstart
* @create 2020-08-16 20:39
*/
public class allFind {
@Test
public void test() {
int[] array = {135,242,192,93,345,11,24,19,19,19,19,19};
majority(array,0);
}
public int[] _elem = new int[8];
public Boolean majority(int[] A,int maj){
maj = majEleCandidate(A);
System.out.println(maj);
return majEleCheck(A,maj);
}
public Boolean majEleCheck(int[] A,int maj){
int occurrence = 0;
for (int i = 0;i < A.length;i++){
if (A[i] == maj) occurrence++;
}
return (2*occurrence > A.length);
}
public int majEleCandidate(int[] A){
int maj = 0;
for (int c = 0,i = 0; i < A.length;i++){
if (0 == c){
maj = A[i];
c = 1;
} else {
if (maj == A[i]) {
c++;
} else {
c--;
}
}
}
return maj;
}
}
中位数

蛮力算法

/**
* 蛮力算法
* @param s1
* @param lo1
* @param n1
* @param s2
* @param lo2
* @param n2
* @return
*/
public int trivialMedian(int[] s1,int lo1,int n1,int[] s2,int lo2,int n2){
int hi1 = lo1 + n1,hi2 = lo2 + n2;
Vector s = new Vector();
while ((lo1 < hi1) && (lo2 < hi2)){
while ((lo1 < hi1) && (s1[lo1] <= s2[lo2])) s.add(s1[lo1++]);
if (lo1 == 8) break;
//以免出现越界,可能换成向量不用写这个
while ((lo2 < hi2) && (s2[lo2] <= s1[lo1])) s.add(s2[lo2++]);
}
while (lo1 < hi1) s.add(s1[lo1++]);
while (lo2 < hi2) s.add(s2[lo2++]);
return (int) s.elementAt((n1 + n2 +1)/2);
}
两个都为n


/**
* 子串的长度相同
* @param s1
* @param lo1
* @param s2
* @param lo2
* @param n
* @return
*/
public int median1(int[] s1,int lo1,int[] s2,int lo2,int n){
if (n < 3) return trivialMedian(s1,lo1,n,s2,lo2,n);
int mi1 = lo1 + n / 2,mi2 = lo2 + (n - 1)/2;
if (s1[mi1] < s2[mi2]){
return median1(s1,mi1,s2,lo2,n + lo1 - mi1);
} else if (s1[mi1] > s2[mi2]){
return median1(s1,lo1,s2,mi2,n + lo2 -mi2);
} else {
return s1[mi1];
}
}
一般情况


public int median2(int[] s1,int lo1,int n1,int[] s2,int lo2,int n2){
if (n1 > n2) return median2(s2,lo2,n2,s1,lo1,n1);
//因为下面仅针对n1 <= n2的情况在讨论
if (n2 < 6) //蛮力算法
return trivialMedian(s1,lo1,n1,s2,lo2,n2);
if(2 * n1 < n2){
//若两个向量的长度相差悬殊,则长者(S2)的两翼可直接截除
return median2(s1,lo1,n1,s2,lo2 + (n2 - n1 -1)/2,n1 + 2 - (n2 -n1)%2);
//这里怎么取两边的可以看一下
}
int mi1 = lo1 + n1/2;
int mi2a = lo2 + (n1 - 1)/2;
//这里其实是保证截取的左右平衡
int mi2b = lo2 + n2 -1 - n1/2;
if (s1[mi1] > s2[mi2b]){
return median2(s1,lo1,n1/2 + 1,s2,mi2a,n2 - (n1 - 1)/2);
} else if (s1[mi1] < s2[mi2a]){
return median2(s1,mi1,(n1+1)/2,s2,lo2,n2 - n1/2);
} else {
return median2(s1,lo1,n1,s2,mi2a,n2 - (n1 - 1)/2 *2);
}
}
总的
package com.atguigu.sort;
import org.junit.Test;
import java.util.Vector;
/**
* @anthor shkstart
* @create 2020-08-16 21:07
*/
public class middleFind {
@Test
public void test(){
int[] array1 = {1,2,3,4,5,6,7,8};
int[] array2 = {9,10,11,12,13,14,15,16};
System.out.println(trivialMedian(array1,0,8,array2,0,8));
}
/**
* 蛮力算法
* @param s1
* @param lo1
* @param n1
* @param s2
* @param lo2
* @param n2
* @return
*/
public int trivialMedian(int[] s1,int lo1,int n1,int[] s2,int lo2,int n2){
int hi1 = lo1 + n1,hi2 = lo2 + n2;
Vector s = new Vector();
while ((lo1 < hi1) && (lo2 < hi2)){
while ((lo1 < hi1) && (s1[lo1] <= s2[lo2])) s.add(s1[lo1++]);
if (lo1 == 8) break;
//以免出现越界,可能换成向量不用写这个
while ((lo2 < hi2) && (s2[lo2] <= s1[lo1])) s.add(s2[lo2++]);
}
while (lo1 < hi1) s.add(s1[lo1++]);
while (lo2 < hi2) s.add(s2[lo2++]);
return (int) s.elementAt((n1 + n2 +1)/2);
}
/**
* 子串的长度相同
* @param s1
* @param lo1
* @param s2
* @param lo2
* @param n
* @return
*/
public int median1(int[] s1,int lo1,int[] s2,int lo2,int n){
if (n < 3) return trivialMedian(s1,lo1,n,s2,lo2,n);
int mi1 = lo1 + n / 2,mi2 = lo2 + (n - 1)/2;
if (s1[mi1] < s2[mi2]){
return median1(s1,mi1,s2,lo2,n + lo1 - mi1);
} else if (s1[mi1] > s2[mi2]){
return median1(s1,lo1,s2,mi2,n + lo2 -mi2);
} else {
return s1[mi1];
}
}
public int median2(int[] s1,int lo1,int n1,int[] s2,int lo2,int n2){
if (n1 > n2) return median2(s2,lo2,n2,s1,lo1,n1);
//因为下面仅针对n1 <= n2的情况在讨论
if (n2 < 6) //蛮力算法
return trivialMedian(s1,lo1,n1,s2,lo2,n2);
if(2 * n1 < n2){
//若两个向量的长度相差悬殊,则长者(S2)的两翼可直接截除
return median2(s1,lo1,n1,s2,lo2 + (n2 - n1 -1)/2,n1 + 2 - (n2 -n1)%2);
//这里怎么取两边的可以看一下
}
int mi1 = lo1 + n1/2;
int mi2a = lo2 + (n1 - 1)/2;
//这里其实是保证截取的左右平衡
int mi2b = lo2 + n2 -1 - n1/2;
if (s1[mi1] > s2[mi2b]){
return median2(s1,lo1,n1/2 + 1,s2,mi2a,n2 - (n1 - 1)/2);
} else if (s1[mi1] < s2[mi2a]){
return median2(s1,mi1,(n1+1)/2,s2,lo2,n2 - n1/2);
} else {
return median2(s1,lo1,n1,s2,mi2a,n2 - (n1 - 1)/2 *2);
}
}
}
基于优先级队列
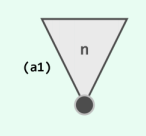
第一种算法如图(a1)所示。首先,花费O(n)时间将全体元素组织为一个小顶堆;然后,经
过k次delMin()操作,则如图(a2)所示得到位序为k的元素
@Test
public void test1() {
Integer[] array = {135,242,192,93,345,11,24,19,19,19,19,19};
PQ_CompHeap pq = new PQ_CompHeap(array,4);
for (int i = 0;i < array.length;i++){
pq.insert(array[array.length - 4 -1 + i]);
pq.delMax();
}
System.out.println(pq.getMax());
}

任取k个元素,并在O(k)时间以内将其组织为大顶堆。然后将剩余的n - k个元素逐个插入堆中;每插入一个,随即删除堆顶,以使堆的规模恢复为k。待所有元素处理完毕之后,堆顶即为目标元素
@Test
public void test2() {
Integer[] array = {135,242,192,93,345,11,24,19,19,19,19,19};
PQ_CompHeap pq = new PQ_CompHeap(array,array.length);
for (int i = 0;i < 6;i++){
pq.delMin();
}
System.out.println(pq.getMin());
}
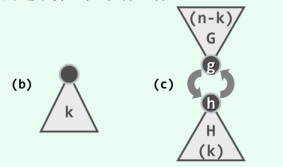
首先将全体元素分为两组,分别构建一个规模为n - k的小顶堆G和一个规模为k的大顶堆H。接下来,反复比较它们的堆顶g和h,只要g < h,则将二者交换,并重新调整两个堆。如此,G的堆顶g将持续增大,H的堆顶h将持续减小。当g>=h时,h即为所要找的元素
@Test
public void test3() {
Integer[] array1 = {135,242,192,93,345,11,24,19,19,19,19,19};
Integer[] array2 = new Integer[array1.length - 4];
for (int i = 4;i < array1.length;i++){
array2[i-4] = array1[i];
}
PQ_CompHeap pq1 = new PQ_CompHeap(array2,array1.length - 4);
PQ_CompHeap pq2 = new PQ_CompHeap(array1,4);
while (pq1.getMin() < pq2.getMax()){
swap(pq1.getMin(),pq2.getMax());
}
System.out.println(pq2.getMax());
}
public void swap(Integer a,Integer b){
Integer c = a;
a = b;
b = c;
}
基于快速划分
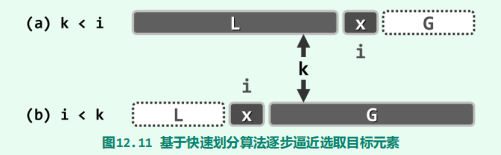
调用算法partition()构造向量A的一个轴点A[i] = x。若i =k,则该轴点恰好就是待选取的目标元素,即可直接将其返回;没有的话,相应减去不可能包含的部分如L段、G段


K-选取算法

package com.atguigu.sort;
import org.junit.Test;
import java.util.Vector;
/**
* @anthor shkstart
* @create 2020-08-18 8:34
*/
public class K_Find {
@Test
public void test(){
int[] array = {135,242,192,93,345,11,24,19};
}
public static int Q = 5;
public int select(Vector A, int k){
if (A.size() < Q){
return trivialSelect(A,k);
}
Vector B = new Vector();
int[] C = new int[Q];
for (int i = 1;i <= A.size()/Q;i++){
for (int j = (i-1) * Q;j < Q*i;j++){
C[j - (i-1) * Q] =(int) A.elementAt((i-1) * Q);
}
sort(C);
B.add(meddile(C));
}
int m = select(B,C.length/2);
int i = 0;
Vector l = new Vector();
int e = 0;
Vector g = new Vector();
while (i < A.size()){
if ((int)A.elementAt(i) < m){
l.add((int)A.elementAt(i));
} else if((int)A.elementAt(i) == m){
e++;
} else {
g.add((int)A.elementAt(i));
}
i++;
}
if (l.size() >= k) {
return select(l,k);
} else if (l.size() + e >= k){
return m;
} else {
return select(g,k - l.size() - e);
}
}
public int trivialSelect(Vector A,int k){
return 0;
}
public void sort(int[] A){
}
public int meddile(int[] A){
return 0;
}
}
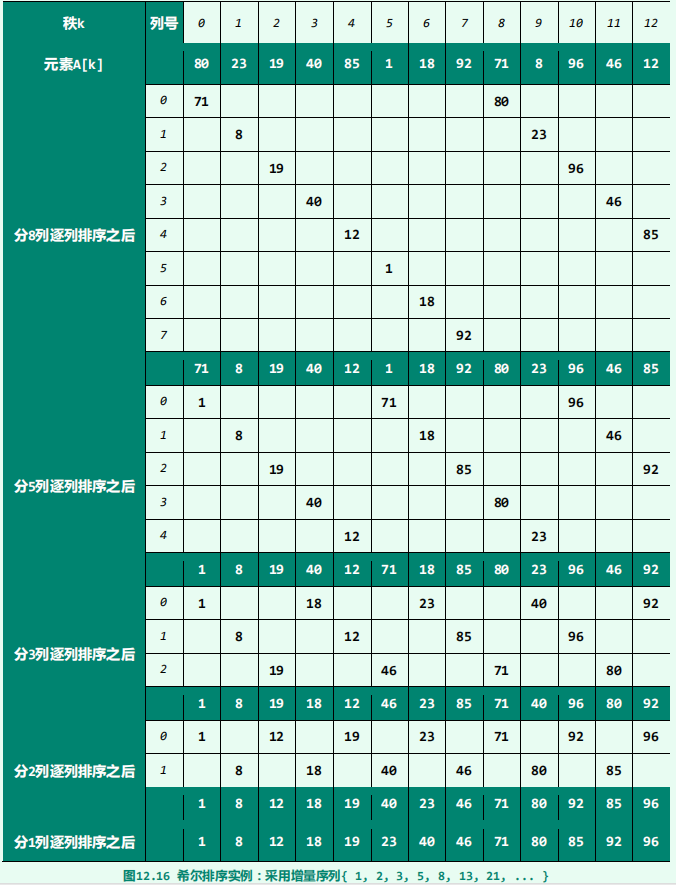
希尔排序
原理
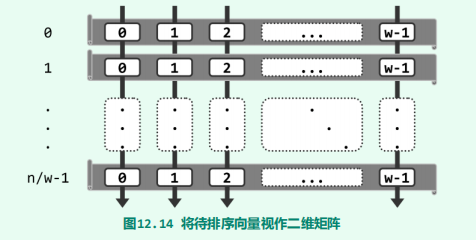


实现(感觉很难按上面的方式写,先复制了一个,以后改)
package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/11/24.
*/
public class ShellSort {
public static void main(String []args){
int []arr ={1,4,2,7,9,8,3,6};
sort(arr);
System.out.println(Arrays.toString(arr));
int []arr1 ={1,4,2,7,9,8,3,6};
sort1(arr1);
System.out.println(Arrays.toString(arr1));
}
/**
* 希尔排序 针对有序序列在插入时采用交换法
* @param arr
*/
public static void sort(int []arr){
//增量gap,并逐步缩小增量
for (int gap=arr.length/2;gap>0;gap/=2){
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for (int i=gap;i<arr.length;i++){
int j = i;
while(j-gap>=0 && arr[j]<arr[j-gap]){
//插入排序采用交换法
swap(arr,j,j-gap);
j-=gap;
}
}
}
}
/**
* 希尔排序 针对有序序列在插入时采用移动法。
* @param arr
*/
public static void sort1(int []arr){
//增量gap,并逐步缩小增量
for (int gap=arr.length/2;gap>0;gap/=2){
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for (int i=gap;i<arr.length;i++){
int j = i;
int temp = arr[j];
if(arr[j]<arr[j-gap]){
while(j-gap>=0 && temp<arr[j-gap]){
//移动法
arr[j] = arr[j-gap];
j-=gap;
}
arr[j] = temp;
}
}
}
}
/**
* 交换数组元素
* @param arr
* @param a
* @param b
*/
public static void swap(int []arr,int a,int b){
arr[a] = arr[a]+arr[b];
arr[b] = arr[a]-arr[b];
arr[a] = arr[a]-arr[b];
}
}
改进


