BZOJ 2440 莫比乌斯函数+容斥+二分

2440: [中山市选2011]完全平方数

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 5473  Solved: 2679
[Submit][Status][Discuss]

Description

小 X 自幼就很喜欢数。但奇怪的是，他十分讨厌完全平方数。他觉得这些
数看起来很令人难受。由此，他也讨厌所有是完全平方数的正整数倍的数。然而
这丝毫不影响他对其他数的热爱。 
这天是小X的生日，小 W 想送一个数给他作为生日礼物。当然他不能送一
个小X讨厌的数。他列出了所有小X不讨厌的数，然后选取了第 K个数送给了
小X。小X很开心地收下了。 
然而现在小 W 却记不起送给小X的是哪个数了。你能帮他一下吗？

Input

包含多组测试数据。文件第一行有一个整数 T，表示测试
数据的组数。 
第2 至第T+1 行每行有一个整数Ki，描述一组数据，含义如题目中所描述。 

Output

含T 行，分别对每组数据作出回答。第 i 行输出相应的
第Ki 个不是完全平方数的正整数倍的数。

Sample Input

4
1
13
100
1234567

Sample Output

1
19
163
2030745

HINT

 对于 100%的数据有 1 ≤ Ki ≤ 10^9,   T ≤ 50

莫比乌斯函数、反演

https://www.cnblogs.com/AOQNRMGYXLMV/p/4065628.html

 题意 输出第ki大的无平方因子数

 解析 无平方因子数可以线性筛，但是筛出来1e9个肯定超时。 我们对答案进行二分mid，转化成求 1~mid 有多少个无平方因子数

根据容斥原理我们可以求出答案，减去(一个素数的平方  的倍数 ）+ 加上（两个素数的乘积 的平方 的倍数）-....+...

比如说100以内 首先删掉  2的平方(4)的倍数 ，3的平方(9)的倍数......   会发现同时为4和9的倍数(e.g. 36 )被删了两遍  所以再把2*3(6)的平方36的倍数加回来. 

要是枚举组合情况太麻烦了 我们发现一个数 a 的容斥系数就是u(a) (莫比乌斯函数) 所以答案就是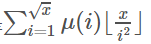   

复杂度O(T*log(n)*sqrt(n))

AC代码

#include <bits/stdc++.h>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define all(a) (a).begin(), (a).end()
#define fillchar(a, x) memset(a, x, sizeof(a))
#define huan printf("
");
#define debug(a,b) cout<<a<<" "<<b<<" ";
using namespace std;
const int maxn=1e5+100,inf=0x3f3f3f3f;
typedef long long ll;
typedef pair<int,int> pii;
int check[maxn],prime[maxn],mu[maxn];
void Mobius(int N)//莫比乌斯函数线性筛
{
    int pos=0;mu[1]=1;
    for (int i = 2 ; i <= N ; i++)
    {
        if (!check[i])
            prime[pos++] = i,mu[i]=-1;
        for (int j = 0 ; j < pos && i*prime[j] <= N ; j++)
        {
            check[i*prime[j]] = 1;
            if (i % prime[j] == 0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[i*prime[j]]=-mu[i];
        }
    }
}int solve(int n)
{
    int temp=sqrt(n),ans=0;
    for(int i=1;i<=temp;i++)
        ans+=mu[i]*n/(i*i);
    return ans;
}
int main()
{
    int t,n;
    Mobius(100000);
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        int l=1,r=2e9,ans;
        while(l<=r)
        {
            int mid=l+(r-l)/2;
            if(solve(mid)>=n) //不能直接等于n 二分的数不一定是无平方因子数
                r=mid-1;
            else
                l=mid+1;
        }
        printf("%d
",r+1);
    }
}