题目
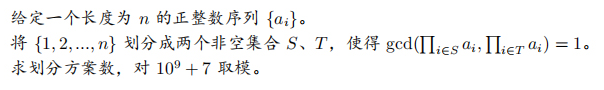
思路
显然任意两个 \(\gcd\) 不为 \(1\) 的数字必须分到一个组里。所以可以在筛质数的同时将有相同质因数的数字归到一个集合内,设最终有 \(m\) 个集合,那么答案为 \(2^m-2\)(减去两个空集合情况)。
我采用埃氏筛 + 并查集,时间复杂度 \(O(n\log \log n)\)。事实上暴力枚举质因数 + dfs 也是可以的。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010,M=1000010,MOD=1e9+7;
int Q,n,m,father[M];
bool vis[M],v[M];
void prework()
{
for (int i=0;i<M;i++)
father[i]=i,vis[i]=v[i]=0;
m=0;
}
int find(int x)
{
return x==father[x]?x:father[x]=find(father[x]);
}
ll fpow(ll x,int k)
{
ll ans=1;
for (;k;k>>=1,x=x*x%MOD)
if (k&1) ans=ans*x%MOD;
return ans;
}
int main()
{
// freopen("data.txt","r",stdin);
scanf("%d",&Q);
while (Q--)
{
prework();
scanf("%d",&n);
for (int i=1,x;i<=n;i++)
{
scanf("%d",&x);
vis[x]=1;
if (x==1) m++;
}
for (int i=2,last;i<M;i++)
{
if (v[i]) continue;
if (vis[i]) last=i;
else last=0;
for (int j=i*2;j<M;j+=i)
{
v[j]=1;
if (vis[j])
{
if (last) father[find(j)]=find(last);
last=j;
}
}
}
for (int i=2;i<M;i++)
if (vis[i] && find(i)==i) m++;
printf("%lld\n",(fpow(2LL,m)-2LL+MOD)%MOD);
}
return 0;
}