【洛谷P6135】【模板】虚树

题目

题目链接：https://www.luogu.com.cn/problem/P6135
给定一棵 \(n\) 个点的有根树，树上有 \(k\) 个关键点，请你构建这些点的虚树。

思路

\(\operatorname{Update:}\)本解法不是虚树的一般解法，只是询问只有一组，所以就直接在 dfs 中做完询问。如果本题有 \(m\) 组询问，那依然要用一般方法，否则时间复杂度为 \(O(nm\log n)\)。
虚树指的是一棵仅包含这些关键节点以及他们两两之间的 LCA 的树。其中一条树边的权值为原树的两点之间权值之和。
考虑用 dfs 遍历原树，用一个栈维护从根节点到最近一次到达的关键节点之间的关键节点路径。例如下图

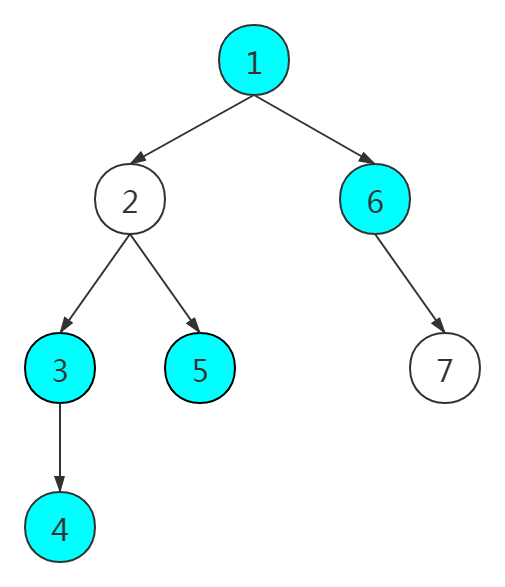
蓝色节点为关键节点，假设我们现在遍历到 4，那么栈 \(s=[1,3,4]\)。
当我们遍历到一个关键节点 \(x\) 时，设栈顶元素为 \(y\)，\(x,y\) 的 LCA 为 \(p\)。

• 如果 \(p=y\)，那么 \(x\) 就是 \(y\) 子树下的点，直接在栈中插入 \(x\) 即可。
• 如果 \(p≠y\)，那么 \(x,y\) 应该是 \(p\) 子树下的两个节点。例如上图我们遍历到节点 5 时，\(x=5,y=4,p=2\)，则节点 4、5 都是 2 的子树下的节点。
  那么我们就不断弹出栈顶，弹出 \(s[top]\) 前将虚树中连边 \((s[top-1],s[top])\)。直到栈顶第二个元素的深度不小于 \(p\) 的深度为止。
  此时将栈顶元素与 \(p\) 连边，并弹出栈顶。注意此时 \(p\) 可能不在栈中，如果不在栈中就插入 \(p\)。最后再插入 \(x\)，继续往下。

最后 dfs 完毕时将栈内的元素再次两两连边即可。时间复杂度 \(O(n\log n)\)。
为了防止栈中没有元素，我们可以现在栈中插入 0 当做一个超级根。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=200010,LG=20;
int n,m,tot,top,rt,fa[N],head[N],s[N],f[N][LG+1],dep[N];
bool key[N];

struct edge
{
	int next,to;
}e[N];

void add(int from,int to)
{
	e[++tot].to=to;
	e[tot].next=head[from];
	head[from]=tot;
}

int lca(int x,int y)
{
	if (dep[x]<dep[y]) swap(x,y);
	for (int i=LG;i>=0;i--)
		if (dep[f[x][i]]>=dep[y]) x=f[x][i];
	if (x==y) return x;
	for (int i=LG;i>=0;i--)
		if (f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	return f[x][0];
}

void dfs(int x,int ff)
{
	dep[x]=dep[ff]+1; f[x][0]=ff;
	for (int i=1;i<=LG;i++)
		f[x][i]=f[f[x][i-1]][i-1];
	if (key[x])
	{
		int p=lca(x,s[top]);
		if (p!=s[top])
		{
			while (dep[s[top-1]]>dep[p])
			{
				fa[s[top]]=s[top-1];
				top--;
			}
			fa[s[top]]=p; top--;
			if (s[top]!=p) s[++top]=p;
		}
		s[++top]=x;
	}
	for (int i=head[x];~i;i=e[i].next)
		dfs(e[i].to,x);
}

int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	for (int i=1,x;i<=n;i++)
	{
		scanf("%d",&x);
		if (x) add(x,i);
			else rt=i;
	}
	for (int i=1,x;i<=m;i++)
	{
		scanf("%d",&x);
		key[x]=1;
	}
	memset(fa,-1,sizeof(fa));
	top=1;
	dfs(rt,0);
	for (int i=top;i>=1;i--)
		fa[s[i]]=s[i-1];
	for (int i=1;i<=n;i++)
		if (fa[i]==-1) printf("-1 -1\n");
		else if (!fa[i]) printf("0 0\n");
		else printf("%d %d\n",fa[i],dep[i]-dep[fa[i]]);
	return 0;
}