题目:
Given numRows, generate the first numRows of Pascal's triangle.
For example, given numRows = 5,
Return
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
题解:
既然讲到了Pascal‘s Triangle,即杨辉三角。那么就先去Wikipedia上面复习一下杨辉三角吧:
”杨辉三角形,又称賈憲三角形、帕斯卡三角形、海亚姆三角形,是二项式係數在的一种写法,形似三角形。
杨辉三角形第n层(顶层称第0层,第1行,第n层即第n+1行,此处n为包含0在内的自然数)正好对应于二项式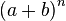 展开的系数。例如第二层1 2 1是幂指数为2的二项式
展开的系数。例如第二层1 2 1是幂指数为2的二项式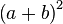 展开形式
展开形式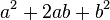 的系数。
的系数。
杨辉三角的性质:
- 楊輝三角以正整數構成,數字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 個數字為組合數
個數字為組合數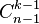 。
。 - 第
 行数字和为
行数字和为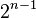 。
。 - 除每行最左側與最右側的數字以外,每个数字等于它的左上方與右上方两个数字之和(也就是說,第
 行第
行第 個數字等於第
個數字等於第 行的第
行的第 個數字與第
個數字與第 個數字的和)。這是因为有組合恒等式:
個數字的和)。這是因为有組合恒等式: 。可用此性质写出整个楊輝三角形。
。可用此性质写出整个楊輝三角形。
”
根据上面那个图,我们可以发现,第一行和第二行都由1组成。其他行的起始和结束都是1.内容由上一行相邻两个数组和组成。由此我们可以写出代码。
代码如下:
1 public class Solution {
2 public static List<List<Integer>> generate(int numRows) {
3 List<List<Integer>> res = new ArrayList<List<Integer>>();
4
5 if(numRows == 0)
6 return res;
7
8 for(int j = 0;j<numRows;j++){
9 List<Integer> row = new ArrayList<Integer>();
10 row.add(1);
11 for(int i=1;i<j;i++){//除去第一行和第二行才进这个循环
12 List<Integer> prevRow = res.get(j-1);//当前行的上一行
13 int temp = prevRow.get(i-1)+prevRow.get(i);
14 row.add(temp);
15 }
16 if(j!=0)//除了第一行,末尾接个1
17 row.add(1);
18 res.add(row);
19 }
20 return res;
21 }
2 public static List<List<Integer>> generate(int numRows) {
3 List<List<Integer>> res = new ArrayList<List<Integer>>();
4
5 if(numRows == 0)
6 return res;
7
8 for(int j = 0;j<numRows;j++){
9 List<Integer> row = new ArrayList<Integer>();
10 row.add(1);
11 for(int i=1;i<j;i++){//除去第一行和第二行才进这个循环
12 List<Integer> prevRow = res.get(j-1);//当前行的上一行
13 int temp = prevRow.get(i-1)+prevRow.get(i);
14 row.add(temp);
15 }
16 if(j!=0)//除了第一行,末尾接个1
17 row.add(1);
18 res.add(row);
19 }
20 return res;
21 }