1232 Check If It Is a Straight Line 缀点成线
问题描述
在一个 XY 坐标系中有一些点,我们用数组 coordinates 来分别记录它们的坐标,其中 coordinates[i] = [x, y] 表示横坐标为 x、纵坐标为 y 的点。
请你来判断,这些点是否在该坐标系中属于同一条直线上,是则返回 true,否则请返回 false。
示例 1:
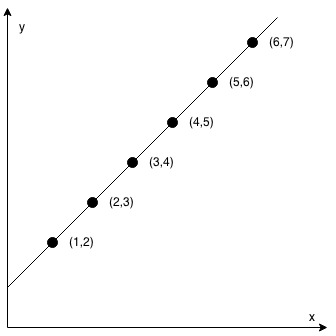
输入: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
输出: true
示例 2:
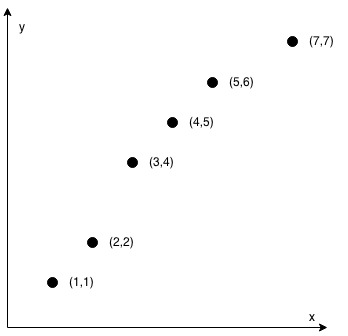
输入: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
输出: false
提示:
2 <= coordinates.length <= 1000coordinates[i].length == 2-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4coordinates中不含重复的点
思路
- 读题
连点成线, 一条线上的点有什么特点? 斜率相等
暴力法 因为点不多(1000以内)
枚举这条线的状态: 斜的/平的/竖的
- 平的: y值相等
- 竖的: x值相等
- 斜的: 斜率
(y1-y2)/(x1-x2)相等
公式法 y=kx+b
通过两个点, 确定k, b的值, 建立直线公式y=kx+b
将剩余点逐一代入公式
代码实现
暴力法
class Solution {
public boolean checkStraightLine(int[][] coordinates) {
int len = coordinates.length;
// x轴是否相等
int linex = coordinates[0][0];
boolean yes = true;
for (int i = 1; i < len; i++) {
if (coordinates[i][0] != linex) {
yes = false;
break;
}
}
// 如果x值全相等 竖线
if (yes) return true;
// y轴是否相等
int liney = coordinates[0][1];
yes = true;
for (int i = 1; i < len; i++) {
if (coordinates[i][1] != liney) {
yes = false;
break;
}
}
// 如果y值全相等 横线
if (yes) return true;
// 斜线
int dx = coordinates[1][0]-coordinates[0][0], x1 = coordinates[0][0];
int dy = coordinates[1][1]-coordinates[0][1], y1 = coordinates[0][1];
if (dx == 0 || dy == 0) {
return false;
}
// 初始斜率
double dxy = dx/dy;
for (int i = 2; i < len; i++) {
int curx = coordinates[i][0], cury = coordinates[i][1];
// 因为不可能出现斜率为0(竖线/横线)
if ((curx-x1) == 0 || (cury-y1) == 0) {
return false;
}
// 当前点斜率
double dcp = (curx-x1)/(cury-y1);
if (dxy == dcp) {
continue;
}
return false;
}
return true;
}
}
公式法
class Solution {
public boolean checkStraightLine(int[][] coordinates) {
int len = coordinates.length;
// 两点必定一线
if (len <= 2) {
return true;
}
int x1 = coordinates[0][0], y1 = coordinates[0][1];
int x2 = coordinates[1][0], y2 = coordinates[1][1];
// y = kx+b --> k = (y1-y2)/(x1-x2) b = y-kx
int k, b;
if (x1 == x2) {
k = 0;
} else {
k = (y1-y2)/(x1-x2);
}
b = y1 - k*x1;
for (int i = 3; i < len; i++) {
int y = coordinates[i][1], x = coordinates[i][0];
if (y != k*x + b) {
return false;
}
}
return true;
}
}