常用的数据结构（图）

1.图结构，非线性数据类型

• 图结构包括顶点(Vertex)和边(Edge)，可以没有边，但至少要有一个顶点。
• 顶点的度(D(V))：连接某个点的边数，有向的分入度(ID(V))和出度(OD(V))。
• 无向图是互为邻接顶点有向图有入边邻接顶点和出边邻接顶点。
• 无向完全图和有向完全图，就是每一个顶点都连接着另外的所有顶点。
• 子图就是

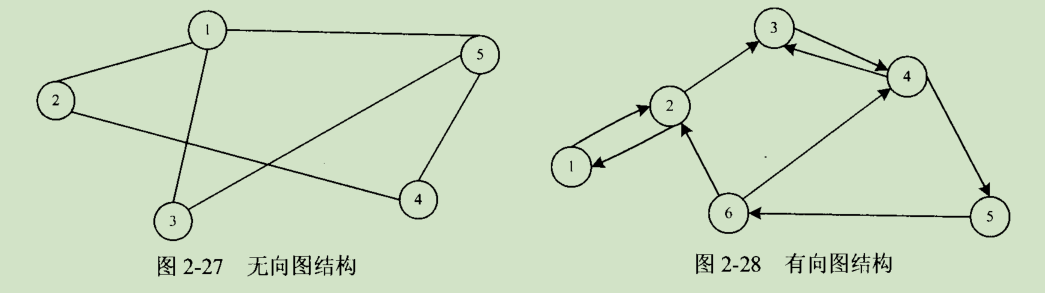
• 无向和有向图的顶点集合和边集合分别是：
  

  无向结构图：
  V(G)={V1, V2, V3, V4, V5, V6}
  E(G)={(V1, V2), (V1, V5), (V2, V4), (V3, V5), (V4, V5), (V1, V3)}
  
  有向结构图：
  V(G)={V1, V2, V3, V4, V5, V6}
  E(G)={<V1, V2>, <V2, V1>, <V2, V3>, <V3, V4>, <V4, V3>, <V4, V5>, <V5, V6>, <V6, V4>, <V6, V2>}

• 路径和路径长度：路径(V5, V1)、(V1, V2),途经顶点V1，路径长度为2(经过了两个边，)
  • 简单路径(路径上顶点不重复出现)
  • 环/回路(路径的第一个顶点和最后一个顶点相同)
  • 简单环路(除第一个顶点和最后一个顶点相同，其他顶点不重复)
• 连通，连通图，连通分量，强连通图和强连通分量
  
  • 连通：两个顶点间有路径，就称两个顶点连通。可途径多个顶点。
  • 连通图：无向图中，任意两个顶点时连通的。如果含有两个顶点是不连通的，称为非连通图。
    
  • 连通分量：无向图的极大连通子图成为该图的连通分量。连通图的连通分量只有一个即本身。
  • 强连通图和强连通分量则是对于有向连通图的，要注意有向连接图的边是有方向的，V1到V2是连通的，但V2到V1不一定是连通的。
• 权（Weight）

　　将边表示成某种数值，这个数字便是该边的权(Weight)。无向图中加入权图，称为无向带权图有向图中加入权值，称为有向带权图。

• 网（Network）

　　网是边上带有权值的图的另一种名称，网与实际应用更加贴切。

 2.java实现图结构

package com.sjx.test1;

import java.util.Scanner;

class GraphMatrix
{
    static final int MaxNum = 20;
    static final int MaxValue = 65535;
    char[] Vertex=new char[MaxNum];
    int GType;
    int VertexNum;    
    int EdgeNum;
    int[][] EdgeWeight = new int[MaxNum][MaxNum];
    int[] isTrav = new int[MaxNum];
}


public class Graph 
{
    static Scanner input = new Scanner(System.in);
    static void CreateGraph(GraphMatrix GM)
    {
        int i, j, k;
        int weight;
        char EstartV, EendV;
        
        System.out.printf("输入图中各个顶点的信息
");
        for(i=0; i<GM.VertexNum; i++)
        {
            System.out.printf("第%d个顶点,请输入第%d个顶点的名称：",i+1, i+1 );
            GM.Vertex[i]= (input.next().toCharArray())[0];
        }
        System.out.printf("输入构成各边的顶点及权值：
");
        for(k=0; k<GM.EdgeNum; k++)
        {
            System.out.printf("第%d条边: ", k+1);
            System.out.printf("
第%d条边的起点名称:", k+1);
            EstartV=input.next().charAt(0);
            System.out.printf("
第%d条边的终点名称:", k+1);
            EendV=input.next().charAt(0);
            System.out.printf("
小伙子，输入你想要在%d这条边上存什么(仅限整数)", k+1);
            weight = input.nextInt();
            
            //找到与名称相符的两个顶点所对应的二位数组，也就是保存权的位置
            for(i=0; EstartV!=GM.Vertex[i]; i++);
            for(j=0; EendV!=GM.Vertex[j]; j++);
            GM.EdgeWeight[i][j]=weight;
            if(GM.GType==0)
            {
                System.out.printf("这是一个有向图，还需要输入两个顶点间的另一条边的权，"
                        + "只不过在这里不用你输入了，两条边都给你存储的同样的值。");
                GM.EdgeWeight[j][i]=weight;
            }
        }
    }
    
    static void ClearGraph(GraphMatrix GM)
    {
        int i, j;
        for(i=0; i< GM.VertexNum; i++)
        {
            for(j=0; j<GM.VertexNum; j++)
            {
                GM.EdgeWeight[i][j]=GraphMatrix.MaxValue;
            }

        }
    }
    
    static void OutGraph(GraphMatrix GM)
    {
        int i, j;
        System.out.printf("
现在开始打印每个顶点的名称。
");
        for(j=0; j<GM.VertexNum; j++)
        {
            System.out.printf("	%c", GM.Vertex[j]);
        }
        System.out.printf("
依次打印每条边的权
");
        
        for(i=0; i<GM.VertexNum; i++)
        {
            System.out.printf("%c", GM.Vertex[i]);
            for(j=0; j<GM.VertexNum; j++)
            {
                if(GM.EdgeWeight[i][j]==GraphMatrix.MaxValue)
                {
                    System.out.printf("	Z");
                }
                else
                {    
                    System.out.printf("	%d", GM.EdgeWeight[i][j]);                
                }

            }
            System.out.printf("
");
        }            
    }


    /*由于之前在OutGraph函数中就已经将所有的边都初始化为MaxValue，所以
    遍历的时候只要是MaxValue就是该边未被赋值
    */
    static void DeepTraOne(GraphMatrix GM, int n)　　//从第n个结点遍历开始，深度遍历图
    {
        int i;
        GM.isTrav[n]=1;　　//标记该顶点已经处理过　　　　
        System.out.printf("->%c", GM.Vertex[n]);　　//输出结点数据
        
        for(i=0; i<GM.VertexNum; i++)
        {
            if(GM.EdgeWeight[n][i] != GraphMatrix.MaxValue && GM.isTrav[n]==0)
            {
                DeepTraOne(GM,i);　　　　//递归进行遍历
            }
        }
    }

    static void DeepTraGraph(GraphMatrix GM)　　//深度优先遍历
    {
        int i;
        for(i=0; i<GM.VertexNum; i++)
        {
            GM.isTrav[i]=0;    //清楚各顶点的遍历标志(拷贝顶点数组，但是将拷贝后的数组的值都设置为0)
        }
        System.out.printf("深度优先遍历结点:");
        for(i=0; i<GM.VertexNum; i++)
        {
            if(GM.isTrav[i]==0)　　　　//若该定点未遍历
            {
                DeepTraOne(GM, i);　　//调用函数遍历
            }
        }
        System.out.printf("
");
    }

    
    
    
    public static void main(String[] args)
    {
        GraphMatrix GM = new GraphMatrix();
        System.out.printf("输入生成图的类型(0就表示有向图，非0就表示无向图)：");
    
        GM.GType=input.nextInt();    //图的种类
        System.out.printf("输入图的顶点数量:");
        GM.VertexNum=input.nextInt();
        System.out.printf("请输入图的边的数量：");
        GM.EdgeNum=input.nextInt();
        ClearGraph(GM);
        CreateGraph(GM);
        System.out.printf("该图的邻接矩阵数数据如下:
");
        OutGraph(GM);
        DeepTraGraph(GM);
    }
}