Codeforces 902C/901A

传送门：http://codeforces.com/contest/902/problem/C

本题是一个关于“树”的问题。

将一棵高度为h的有根树表示为数列{a_i|i=0,1,2,...,h}，其中a_i是与根结点的距离为i的结点之数目。求：对于给定的数列，其对应的树的构型是否唯一？若不唯一，试构造两棵不同构的树，打印其特征数列{p_i|i=1,2,...,n}，其中，p_i是i的父结点（若i为根结点，则p_i为0）。

首先，按照数列{a}，将树分层：即第i层是与根结点距离为i的结点构成的集合。

考虑在此约束下，一棵树出现异构的情形：当上下层结点存在连接的异构时，树出现异构。此时，上下层的节点数目均不唯一，即a_i>1且a_i-1>1。

首先考虑树的一种构型X，这种构型是将下层的所有结点连接到上层的某一个结点上的。于是，这棵树上的所有结点，或者位于最长路径上，或者是连接在最长路径上的叶结点。例如：

 

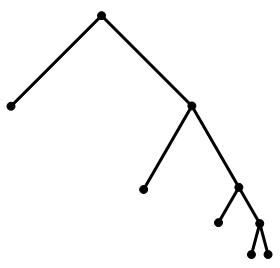
接下来首先讨论本题的案例，给定数列{1,2,2}。可以按照“构型X”构造树如下：

 

这棵树的特征数列为{0,1,1,3,3}，其一种“异构体”如下：

 

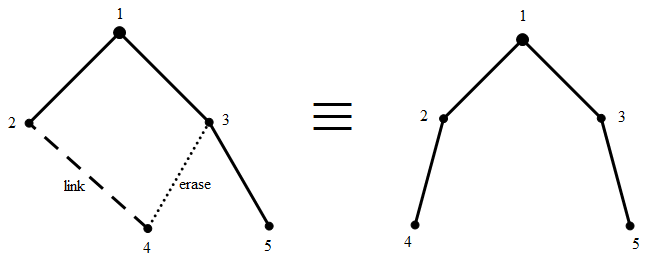
可见，这个“异构体”是将原来的树删除边(3,4)，再连接边(2,4)得到的。其特征数列为{0,1,1,2,3}。

于是，对于一棵“构型X”的树，将其下层的一个结点与上层的一个叶结点构建边，即得到另一种构型的树。于是，可以得到树的两种构型。参考程序如下：

#include <stdio.h>
#define MAX_H 100001
#define MAX_N 200001

int a[MAX_H];
int sum[MAX_H]; //prefix-sum.
int p[2][MAX_N]; //parent of vertex.

int main(void)
{
    int h;
    scanf("%d", &h);
    for (int i = 0; i <= h; i++) {
        scanf("%d", &a[i]);
        //count prefix-sum.
        if (i) sum[i] = sum[i - 1];
        sum[i] += a[i];
    }
    int cur = 1;
    bool flag = true;
    p[0][1] = p[1][1] = 0;
    for (int i = 1; i <= h; i++) {
        for (int j = 0; j < a[i]; j++) {
            cur++;
            p[0][cur] = p[1][cur] = sum[i - 1];
        }
        if (a[i] > 1 && a[i - 1] > 1) {
            flag = false;
            p[1][cur]--;
        }
    }
    if (flag) printf("perfect
");
    else {
        printf("ambiguous
");
        for (int i = 0; i < 2; i++) {
            for (int j = 1; j <= sum[h]; j++)
                printf("%d ", p[i][j]);
            printf("
");
        }
    }
    return 0;
}