三维动画形变算法（Mixed Finite Elements）

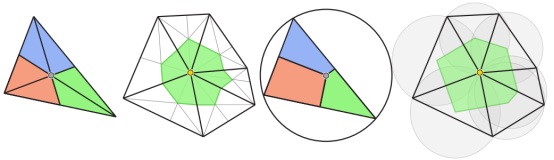
　　混合有限元方法通入引入辅助变量后可以将高阶微分问题变成一系列低阶微分问题的组合。在三维网格形变问题中，我们考虑如下泛函极值问题：

　　其中u: Ω₀ → R³是变形体的空间坐标，上述泛函极值问题对应的欧拉拉格朗日方程就是双调和方程∆²u = 0。

　　通过引入额外变量v，我们可以将上述无约束高阶优化问题转变为带约束的低阶优化问题：

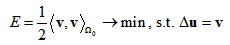
　　引入拉格朗日函数，并利用格林公式可以得到：

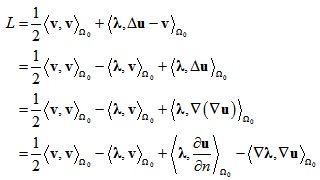
　　将变量v，u，λ写成基函数的线性组合形式，并且基函数选择为分段线性帽函数：

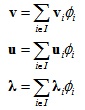
　　将上式分别对变量v_i，u_i，λ_i求偏导可以得到：

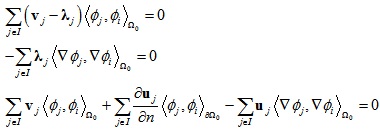
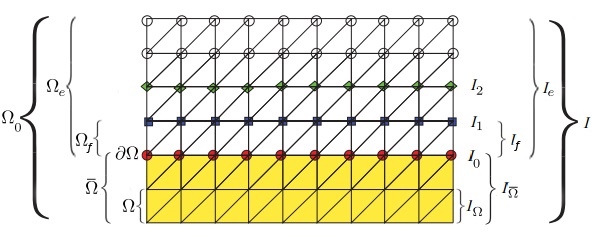
　　这里讨论两种边界条件情况：

　　第一种是固定区域边界条件，就是说在变形体上存在区域Ω_f，其对应的空间位置为u_f：

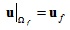
　　求解形式：

　　消除额外变量后得到：

　　

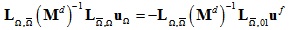
　　第二种是固定曲线边界条件，就是说在变形体上存在曲线C，其满足：

　　求解形式：

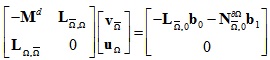
　　消除额外变量后得到：

 

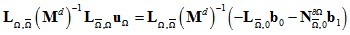
效果：

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。

 

参考文献：

[1] Jacobson A, Tosun E, Sorkine O, et al. Mixed Finite Elements for Variational Surface Modeling. symposium on geometry processing, 2010, 29(5): 1565-1574.

 

附录

基于三维网格的微分问题求解

　　对于求解三维网格上带Dirichlet边界条件的泊松方程：

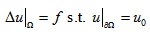
　　将上式写成等价的弱形式：

其中v是任意的测试函数，但是其满足在边界处值为0。

　　利用分部积分，可以将上式等式左边进行变化：

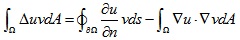
　　由于测试函数在边界处值为0，所以上式中等式右边第一项为0：

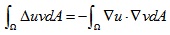
　　然后将待求解函数u和测试函数v表示成基函数的线性组合形式，并且基函数选择为分段线性帽函数：

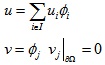
其中I是网格上所有的顶点集合。

　　三维网格上分段线性帽函数如下图所示：

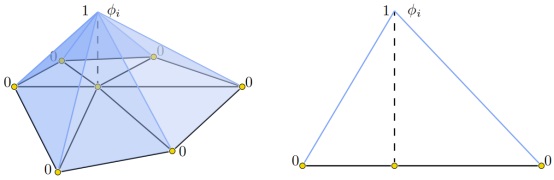
　　那么对于网格内部任意顶点j，我们都取测试函数v = Φ_j，这样可以形成一个方程：

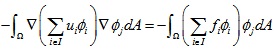
　　将积分里的求和提取到积分外，得到：

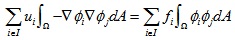
　　由于边界处u的数值已知，那么可以将已知项移到等式右侧：

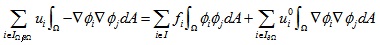
　　这样就形成了n个方程组，n为三维网格除边界外的顶点个数。

　　对于求解三维网格上带Neumann边界条件的泊松方程：

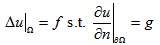
　　同样转换成弱形式，并利用分部积分：

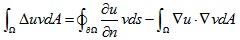
　　在Neumann边界条件下，我们选择边界处值不为0的测试函数，那么可以得到：

 

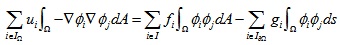
Cotangent权重矩阵L

　　将Φ_i定义为分段线性帽函数，那么矩阵L的具体数值就可以根据三维网格模型唯一确定了，另外矩阵L之所以称为Cotangent权重，是因为其具体表达式是一个三角函数形式。

　　下面具体推导下矩阵L的形式，根据其原始定义表达式：

　　在每个三角片内∇Φ_i是恒定的，并且只有在顶点i相邻的周边三角片上是非零值的。对于一个三角片，∇Φ_i指向的方向与顶点i相对的底边e_i垂直，数值大小为三角片在底边e_i上高h的倒数，即：

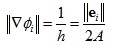
上式中||e_i||是边e_i的长度，A是三角片的面积。

　　对于相邻顶点i和j，∇Φ_i与∇Φ_j的方向分别垂直于各自的底边e_i和e_j，它们之间的夹角记为θ，于是我们可以得到：

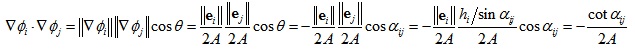
　　由于Φ_i与Φ_j只有在相邻三角片T_α和T_β内才同时为非零值，那么：

 

Mass质量矩阵M

　　矩阵M的原始定义表达式为：

　　由于Φ_i定义为分段线性帽函数，所以M_ij只有当i和j为三维网格上相邻顶点或者i和j相同时其值才为非零。

　　根据积分规则：

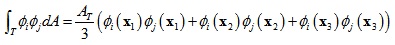
其中A是三角片T的面积，x₁，x₂，x₃是三角片三条边的中点。

　　由于Φ_i在每个三角片内是个简单的线性函数，那么上式可以进一步表示为：

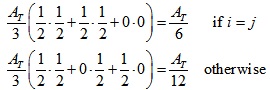
　　于是可以得到矩阵M的表达式：

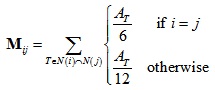
　　通常矩阵M可以用对角矩阵M^d来近似代替，近似过程为：

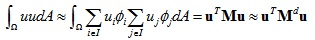
　　矩阵M^d的对角线元素之和等于三维网格Ω的表面积，一般有两种方式来计算对角线元素，分别为重心质量矩阵和Voronoi质量矩阵，如下图所示。