2020icpc上海部分题解

B

题目大意

  给你两张扫雷图A和B，你最多对B修改\(\lfloor \frac{MN}{2} \rfloor\)次，问是否能让B中的数字之和等于A。

解题思路

  扫雷图中的数字等价于相邻的非雷格子与空白格子的对数，相当于一张黑白色的图，很明显，黑白颜色是相对的，即是交换颜色，相邻的黑白颜色的对数也不会改变(就像把黑白对改成白黑对那样)。所以对比两个图中不同的块的个数，如果小于\(\lfloor \frac{MN}{2} \rfloor\)就直接输出A，否则输出A格子翻转之后的图。

代码

const int maxn = 1e3+10;
int n, m;
char g1[maxn][maxn], g2[maxn][maxn], g3[maxn][maxn];
int solve(char ga[maxn][maxn], char gb[maxn][maxn]) {
    int cnt = 0;
    for (int i = 1; i<=n; ++i)
        for (int j = 1; j<=m; ++j)
            if (ga[i][j]!=gb[i][j]) ++cnt;
    return cnt;
}
int main() {
    IOS;
    cin >> n >>m;
    for (int i = 1; i<=n; ++i) cin >> g1[i]+1;
    for (int i = 1; i<=n; ++i) cin >> g2[i]+1;
    for (int i = 1; i<=n; ++i)
        for (int j = 1; j<=m; ++j) {
            if (g1[i][j]=='.') g3[i][j] = 'X';
            else g3[i][j] = '.';
        }
    if (solve(g1, g2)<=n*m/2) {
        for (int i = 1; i<=n; ++i) cout << g1[i]+1 << endl;
    }
    else if (solve(g3, g2)<=n*m/2) {
        for (int i = 1; i<=n; ++i) cout << g3[i]+1 << endl;
    }
    return 0;
}

C

题目大意

  给你两个数X和Y，求下面式子

解题思路

  可以考虑数位dp按位填数，\(i \& j = 0\)说明同一位不同1，而后面的取log相当于求i和j中最高的那个二进制位位数。这样就转换成了一个比较板子的数位dp了，细节可以看注释。

代码

int a[33], b[33];
ll dp[33][2][2][2];
ll solve(int len, int lim1, int lim2, int tp) {
    //tp 0:前面有1 1:前面没有1
	if (len==-1) return 1;
	if (dp[len][lim1][lim2][tp]!=-1) return dp[len][lim1][lim2][tp];
	int up1 = lim1 ? a[len]:1; 
    //如果前面到上限了，只能取当前上限，否则填0和1都可，即当前上限是1
	int up2 = lim2 ? b[len]:1;
	ll res = 0;
	for (int i = 0; i<=up1; ++i)
		for (int j = 0; j<=up2; ++j) {
			if (i&j) continue;
			ll t;
			if (tp&&(i||j)) t = len+1; 
            //如果前面没有1，当前有1，说明当前是最高位，计算log
			else t = 1;
			res = (res+solve(len-1, lim1&&i==up1, lim2&&j==up2, tp&&!i&&!j)*t%MOD)%MOD;
            //lim&&i==up1，如果前面取到上限，并且当前也是上限，对于下一个来说才受限制，否则随便取
		}
	return dp[len][lim1][lim2][tp] = res;
}
int main() { 
	IOS;
	int __; cin >> __;
	while(__--) {
		int x, y; cin >> x >> y;
		int len = 0;
		while(x||y) {
			a[len] = x&1;
			b[len] = y&1;
			x >>= 1;
			y >>= 1;
			++len;
		}
		clr(dp, 0xff);
		cout << ((solve(len-1, 1, 1, 1)-1)%MOD+MOD)%MOD << endl;
        //减1即减去0 0的情况
	}
	return 0;
} 

D

题目大意

  两人站在[0,n]的线段上，一个人站在p1，速度v1，另一个人站在p2，速度v2，问两个人最少需要多少时间使每个点至少被覆盖一遍。

解题思路

  比赛时想着分三段三分相遇的位置，但是不确定函数是否单峰，一直wa个不停，其实可以二分时间，很明显这是有单调性的。我们二分时间，然后计算两个人走的互不交叉并且各包含一个端点的最长路径，看能否把整个线段覆盖就行了。但是这里还有一些坑，就看代码吧。注意最后还要考虑上两人对穿的情况。

代码

const int maxn = 1e3+10;
int main() {
    IOS;
    int __; cin >> __;
    while(__--) {
        double n, p1, v1, p2, v2;
        cin >> n >> p1 >> v1 >> p2 >> v2;
        if(p1>p2) {
            swap(p1,p2);
            swap(v1,v2);
        }
        double l = 0, r = 1e12, ans = 0;
        for (int i = 1; i<=200; ++i) {
            double t = (l+r)/2;
            double l1 = t*v1, l2 = t*v2;
            l1 = max((l1+p1)/2, l1-p1);
			if (l1<p1+eps) l1 = 0; //没贡献
            l2 = max((l2+n-p2)/2, l2-(n-p2));
			if (l2<n-p2) l2 = 0; //没贡献
            if (l1+l2-n>=-eps) ans = t, r = t;
            else l = t;
        }
        ans = min(ans, max(p2/v2, (n-p1)/v1));
        cout << fixed << setprecision(10) << ans << endl;
    }
    return 0;
}

E

解题思路

  从最小的数下手，如果最小的数放在位置i，那么i前面的i-1个数可以随便放，而最小值后面的数字，相当于一个新的排列，我们可以继续从最小的数开始划分，所以可以得到下面的状态转移方程：

\[dp[i] = \sum_{j = i-1}^{i-k} dp[i-j] \times c(i-1, j-1) \times !(j-1) \]

  这是一个O(nk)的做法，我们把柿子变换一下

\[\sum_{j = i-1}^{i-k} dp[i-j] \times c(i-1, j-1) \times !(j-1) \]

\[\sum_{j = i-1}^{i-k} dp[i-j] \times \frac{!(i-1)}{!(j-1) \times !(i-j)} \times !(j-1) \]

\[!(i-1) \times \sum_{j = i-1}^{i-k} \frac{dp[i-j]}{!(i-j)} \]

  我们可以用前缀和来存\(\sum_{j = 1}^{i} \frac{dp[j]}{!j}\)，通过前缀和做差求前k个数，这样的话就省去第二个循环的k次枚举，O(n)得到答案了。

const int maxn = 1e7+10;                                                               
const int maxm = 1e6+10;
int f[maxn], inv[maxn], dp[maxn], sum[maxn];
ll qp(ll x, ll y) {
    ll res = 1;
    while(y) {
        if (y&1) res = res*x%MOD;
        x = x*x%MOD;
        y >>= 1;
    }
    return res;
}
int main() { 
    IOS;
    f[0] = 1;
    for (int i = 1; i<maxn; ++i) f[i] = 1ll*f[i-1]*i%MOD;
    inv[maxn-1] = qp(f[maxn-1], MOD-2);
    for (int i = maxn-2; i>=0; --i) inv[i] = 1ll*(i+1)*inv[i+1]%MOD;
    int n, k; cin >> n >> k;
    dp[0] = sum[0] = 1;
    for (int i = 1; i<=n; ++i) {
        dp[i] = sum[i-1];
        if (i-k-1>=0) dp[i] = (dp[i]-sum[i-k-1]+MOD)%MOD;
        dp[i] = 1ll*dp[i]*f[i-1]%MOD;
        sum[i] = (sum[i-1]+1ll*dp[i]*inv[i]%MOD)%MOD;
        //cout << dp[i] << ' ' << sum[i] << endl;
    }
    cout << dp[n] << endl;
    return 0;   
}   

G

  签到，3的倍数的位置对应偶数，偶数不管乘奇数还是偶数都是偶数。

H

解题思路

  结论应该是比较好猜的：我们把每个人和对应的手抓饭在圆盘上连线，那么这些连线是不会相交的。相应的证明可以看这里。这样的话一共有三种情况，要么顺时针转，要么逆时针转，要么先往一个方向转一个角度，再反过来转另一个角度。我们可以分别对a和b排序，然后假设一个方向为正，枚举第一个人抓的饭或者抓第一个饭的人，计算出正方向每个人抓到饭所需的时间，那么正方向的时间就是最大的那个时间，反方向就是n-正方向最小的那个时间，然后再枚举下两个方向转时的分割点就行了。

代码

const int maxn = 2e5+10;                                                               
const int maxm = 1e6+10;
ll a[maxn], b[maxn], c[maxn];
int main() { 
    IOS;
    int __; cin >> __;
    while(__--) {
        int n, m; cin >> n >> m;
        for (int i = 0; i<m; ++i) cin >> a[i];
        for (int i = 0; i<m; ++i) cin >> b[i];
        sort(a, a+m);
        sort(b, b+m);
        ll ans = 1e18;
        for (int i = 0; i<m; ++i) {
            for (int j = 0; j<m; ++j) c[j] = (b[(j+i)%m]-a[j]+n)%n;
            sort(c, c+m);
            ans = min({ans, c[m-1], n-c[0]});
            for (int j = 0; j<m-1; ++j) ans = min({ans, 2*c[j]+n-c[j+1], 2*(n-c[j+1])+c[j]});
        }
        cout << ans << endl;
    }
    return 0;   
} 

I

题目大意

  给你n个同心圆(圆心0,0)已经n条直线(穿过圆心)，求直线与圆相交的点之间的最小距离之和。

解题思路

  对于两个在同一个圆上的点，他们要么是走所在圆的圆弧，要么往下走绕一圈再上来。对于不再同一个圆上的点，一定是离中心最远的点先沿直径走到和另一个点所在的圆弧，然后就是两个点在同一个圆上的情况。考虑第一种情况往下走绕一圈再上来的走法，假设一定经过若干段圆弧，那么一定存在两个点只走一个圆弧的情况，如下图

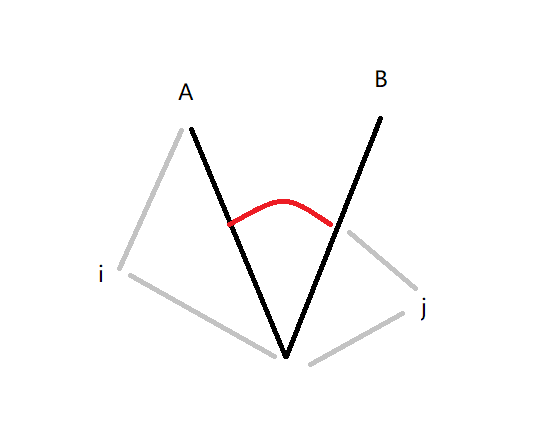
假设从A点下到红色圆弧再回到B是最短路，夹角相当于\(\frac{p \times \pi}{2\times m}\)，那么必有\(2\times j > \frac{p\times 2 \times \pi \times j}{2\times m}\)，化简得到\(2\times m > \pi \times p\)可以发现是走两条长度为j的边还是走圆弧和j的长度是没有关系的，只和角度有关，而且实际走的圆弧应该是AB所在圆的，把j+1可以推出来圆弧越靠上越优，所以我们可以推出位于同一个圆上的两点只有两种走法，满足\(2\times m > \pi \times p\)走两点所在圆的圆弧，否则走半径。

  我们可以枚举每层中的一个点到其他所有点的距离，根据对称性算出这一层的贡献，但是还有更快的方法。我们可以根据层间关系来推，维护两个变量，一个是比现在低一层的那层中的一个点到层数小于等于它的所有点的距离res，一个是res对应的点的个数sum，我们要求当前这一层中的一个点到比他低的点的距离，就可以用res和sum算出来，相当于上一个结果中所有路径往上再走一步。处理完层间的，我们再加上同层的就行了，可以根据上面推出来的结论，预处理出来同层之间需要乘上的系数再乘上半径和点数就可以了。

代码

int main() {
    IOS;
	int n, m; cin >> n >> m;
	double t = 0;
	for (int i = 1; i<m; ++i) {
		if (2.0*m>pi*i) t += pi*2.0*i/m;
		else t += 4;
	}
	t += 2;
	double ans = 0, res = 0, sum = 1;
	for (int i = 1; i<=n; ++i) {
		ans += t*i*m+2*m*(res+sum);
		//t*i*m代表走同一层，res代表靠里那一层一个点到所有小于等于它的那一层的点的距离
		//sum是从这一层的一个点下到比他小的层的点走一步需要多少步
		res += t*i+sum;
		//res从下面一层上来，首先加上sum个1，然后再加上同层的距离
		sum += 2*m;
	}
	if (m==1) ans -= (1+n)*n*m;
	cout << fixed << setprecision(10) << ans << endl;
    return 0;
}

M

解题思路

  先对可以忽略的文件建一棵字典树，要想使ignore的文件数量少，肯定在树上能ignore的最靠上的位置最好。而能ignore的文件肯定不能包含不能ignore的文件，所以我们再把不能ignore的文件插入字典树中，把中间经过的点标记一下，然后我们对字典树dfs一下，走到未标记的点就+1然后不再往下走，最后就能得到答案。

代码

const int maxn = 1e3+10;                                                               
const int maxm = 2e6+10;
int tr[maxn][27], f[maxn], son[maxn], idx;
void insert(string t, int flag) {
    int p = 0;
    for (auto ch : t) {
        ++son[p];
        int tt = ch-'a';
        if (ch=='/') tt = 26;
        if (!tr[p][tt]) tr[p][tt] = ++idx;
        p = tr[p][tt];
        //cout << p << endl;
        f[p] = flag;
    }
    //cout << "________" << endl;
    ++son[p];
}
ll ans;
void dfs(int u) {
    for (int i = 0; i<27; ++i)
        if (tr[u][i]) {
            if (i==26 && !f[tr[u][i]]) ++ans;
            else dfs(tr[u][i]);
        }
}
int main() { 
    IOS;
    int __; cin >> __;
    while(__--) {
        idx = 0; f[0] = 1;
        int n, m; cin >> n >> m;
        for (int i = 1; i<=n; ++i) {
            string s; cin >> s;
            s += '/';
            insert(s, 0);
        }
        for (int i = 1; i<=m; ++i) {
            string s; cin >> s;
            s += '/';
            insert(s, 1);
        }
        ans = 0;
        dfs(0);
        cout << ans << endl;
        for (int i = 0; i<=idx; ++i) son[i] = f[i] = 0, clr(tr[i], 0);
    }
    return 0;   
}