递归函数

递归函数：

　　定义：在函数中调用自身函数就是递归函数 

　　#如果递归次数太多，就不适用递归来解决问题

            #缺点：占内存

            #优点：会让代码变简单

　　递归的最大深度——997 :递归函数如果不受到外力的阻止会一直执行下去。但是每一次函数调用都会产生一个属于它自己的名称空间，如果一直调用下去，就会造成名称空间占用太多内存的问题，于是python为了杜绝此类现象，强制的将递归层数控制在了997,超出997就会提示一下报错内容：

　　　　　　　RecursionError:递归错误，超过了递归的最大深度

def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)


#结果：
997
Traceback (most recent call last):
  File "/Users/yaoyeshiguang/PycharmProjects/S9/day2/ceshi.py", line 79, in <module>
    foo(1)
  File "/Users/yaoyeshiguang/PycharmProjects/S9/day2/ceshi.py", line 77, in foo
    foo(n)
  File "/Users/yaoyeshiguang/PycharmProjects/S9/day2/ceshi.py", line 77, in foo
    foo(n)
  File "/Users/yaoyeshiguang/PycharmProjects/S9/day2/ceshi.py", line 77, in foo
    foo(n)
  [Previous line repeated 993 more times]
  File "/Users/yaoyeshiguang/PycharmProjects/S9/day2/ceshi.py", line 75, in foo
    print(n)
RecursionError: maximum recursion depth exceeded while calling a Python object

997是python为了程序的内存优化所设定的一个默认值，也可以取调整修改该默认值：

#修改递归最大深度为10w
import sys
print(sys.setrecursionlimit(100000))

import sys
sys.setrecursionlimit(1000000)
n = 0
def story():
    global n
    n += 1
    print(n)
    story()

story()


#结果:
...
34939
34940
34941

注：实际可以达到的深度取决于计算机的性能!

　　实例演示：

　　　　　　有四个数，其中第一个为10，第二个比第一个多2，第三个比第二个多2，第四个比第三个多2，问第四个数是多少

#分析规律
a(3) = a(2) + 2
a(2) = a(1) + 2
a(1) = a + 2
a = 10

函数实现如下：

def a(n):
    if n == 1:
        return 10
    else:
        return a(n-1)+2

print(a(4))    #结果16

#代码拆分理解
#a(4) 调用函数a并传入参数4，函数运行结果为return a(4-1)+2，此时尚未等到return返回值再次调用函数a(4-1)即a(3)...以此类推，直至a(1)，n接收的传入参数为1时，满足条件if n==1:执行return 10，此时10作为返回值返给调用函数a(1)即a(2-1)、、、以此类推，逐层将值进行返还，直至a(4)层级，此时结果为10+2+2+2等于16

　　实例进阶

　　　　递归函数与三级菜单

menu = {
    '北京': {
        '海淀': {
            '五道口': {
                'soho': {},
                '网易': {},
                'google': {}
            },
            '中关村': {
                '爱奇艺': {},
                '汽车之家': {},
                'youku': {},
            },
            '上地': {
                '百度': {},
            },
        },
        '昌平': {
            '居庸关': {},
            '天通苑': {},
            '回龙观': {},
        },
        '朝阳': {},
        '东城': {},
    },
    '上海': {
        '闵行': {
            "人民广场": {
                '炸鸡店': {}
            }
        },
        '闸北': {
            '火车战': {
                '携程': {}
            }
        },
        '浦东': {},
    },
    '山东': {},
}


def threeLM(dic):
    while True:
        for k in dic:print(k)
        key = input('input>>').strip()
        if key == 'b' or key == 'q':return key
        elif key in dic.keys() and dic[key]:
            ret = threeLM(dic[key])
            if ret == 'q':return 'q'
        elif (not dic.get(key)) or (not dic[key]):
            continue

threeLM(menu)

递归函数与二分查找法

　　二分查找法，必须处理有序的列表

　　示例：

　　　　现有列表l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]，假设index查找方法不能使用，由于列表内元素过多，使用for循环效率过低，这时二分查找法就登场了！假设目标为66，先来看一下分析过程：

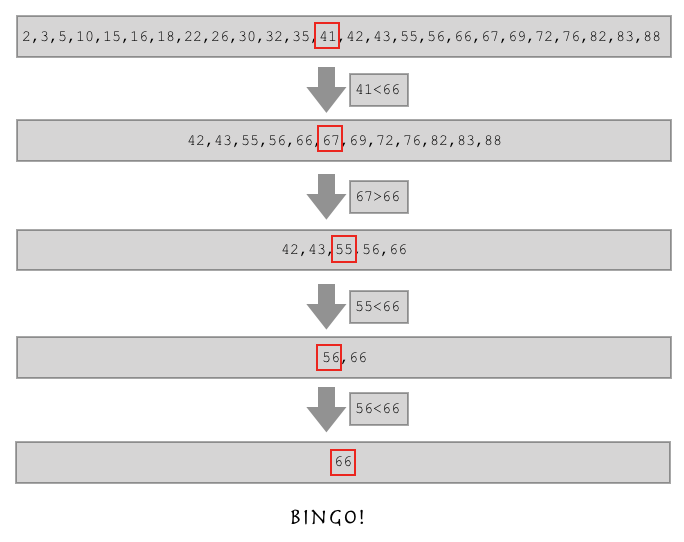
这个过程就是二分查找法，代码落实如下：

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

def func(l,aim):
    mid = (len(l)-1)//2
    if l:
        if aim > l[mid]:
            func(l[mid+1:],aim)
        elif aim < l[mid]:
            func(l[:mid],aim)
        elif aim == l[mid]:
            print("bingo",mid)
    else:
        print('找不到')
func(l,66)
func(l,6)

def search(num,l,start=None,end=None):
    start = start if start else 0
    end = end if end else len(l) - 1
    mid = (end - start)//2 + start   # //2 为除2取整数部分
    if start > end:
        return None
    elif l[mid] > num :
        return search(num,l,start,mid-1)
    elif l[mid] < num:
        return search(num,l,mid+1,end)
    elif l[mid] == num:
        return mid