原文地址:https://zhuanlan.zhihu.com/p/106667070
进入大学,知道要学的课程中有门叫高等数学的,心里就吐槽到:为什么要叫高等数学,难道它要比别的数学高级点迈?

现在想起当时的想法,就一脸无法言喻的笑。
但也没错,高等数学是要比我们中学时期学的数学内容要“高级”点。
在中学时期,我们接触的数学内容,被称为初等数学,就是那些四则运算,方程,基本函数,简单几何,,,,,
而初等数学与高等数学的区别,或者说不同之处,在于两者的研究对象不同。初等数学研究的是不变的量,而高等数学研究的是变动的量(就显得很高级,连变动的事物都能研究出规律。)。
具体一点,比如同样是计算,方程算的是某个固定的量,而函数算的却是变化的量(高中学的函数是初等函数,是函数中的一些典型函数。跟大学里的函数相比,两者像是集合与元素的关系)。
高等数学的学习是基于我们对函数的掌握开展的。
那么到底什么是函数呢?这里我们需要先知道什么是映射(由于函数是映射的一种特殊情况)。

映射,按照字面上的意思,我们可以想象出是某个物体投射到另一个物体的过程。在数学里,映射它也是一个“投射”的过程。
给出官方定义:
假设两个非空集合X、Y,存在一个法则f,使得对X中的每个元素x,按法则f,在Y中有唯一确定的元素y与之对应,那么称f为从X到Y的映射。
(关于定义,我们一定要进行仔细的解读,最好是一句一句的理解,不然之后的学习容易形成概念误差。)
简单的来说,映射它的本质就是一种对应关系。
既然是对应,那前提肯定是得有相互对应的两个事物吧?(所以定义的第一句就是要先有两个非空集合,至于为什么必须是非空集合,你可以想想,都没有东西,你跟啥相对应啊?)
这里有个问题,由于我们之前是先接触的函数内容,所以可能会先入为主的形成一个误区→那就是容易认为映射的两个非空集合都是数集。
其实不是,映射指的是所有的对应关系,不仅仅只是数与数之间的对应关系。
(当然,这可能是因为对集合的概念的理解存在偏差。集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体,比如狗可以形成一个集合,狗窝也可以形成一个集合。而单纯的数,则是数的集合。)
具体举个映射例子,比如狗和狗窝,这两者就可以形成一个居住的对应关系。
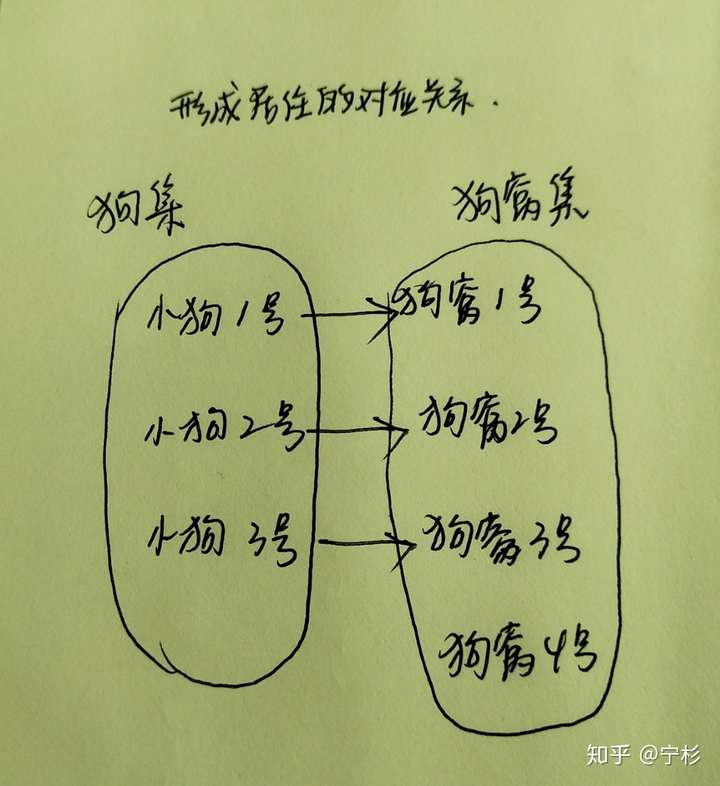
每只狗都要有一个狗窝给它居住,也可以两只狗住同一个狗窝,却不可能一只狗同时住两个狗窝(毕竟它又没有分身术)。
这里把理解对应之前给出的定义就是,
存在一个法则f(也就是对应关系),
使得集合X中的每个元素x(集合X中不可剩余x,要求的是每一个元素。),
在集合Y中有唯一确定的元素y与之对应(如果集合X中有x找不到与之对应元素的y,那么就无法构成映射)。

元素x还有个名字叫原象,与元素x对应的元素y叫x的象(在集合Y中那些没有x与之对应的y不是象),集合X称为映射f的定义域。
象的集合在函数关系中被称为值域,是集合Y的一个子集。

要形成一个映射同时具备三个要素:
1、集合X(定义域)
2、集合Y(值域范围)
3、对应法则f(使得定义域中的每个元素x,有唯一确定的y与之对应)
以上,可以知道,映射就是一种对应关系,而函数只是映射的一种(函数是实数集到实数集的映射)。
对映射有了一定概念后,我们来看一下,映射的三种特殊情况,单射、满射、一一映射(双射)。
(1)单射:设f是集合A到集合B的一个映射,如果对于任意a,b属于A,当a不等于b时有f(a)不等于f(b),则称f是A到B内的单映射 。
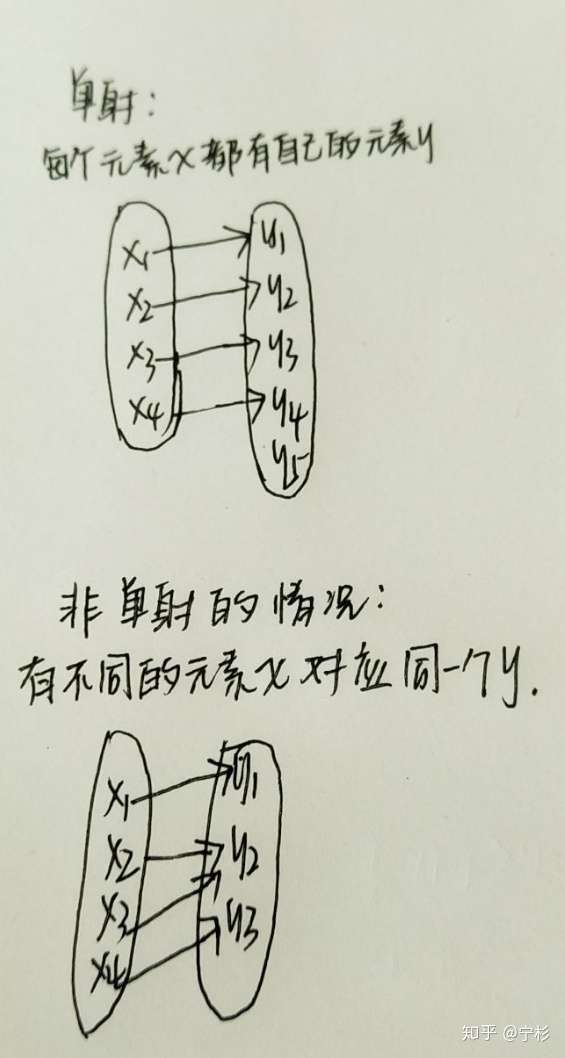
(2)满射:如果对任意的b属于B都有一个a属于A使得f(a)=b,则称f是A到B上的映射,或称f是A到B的满映射。
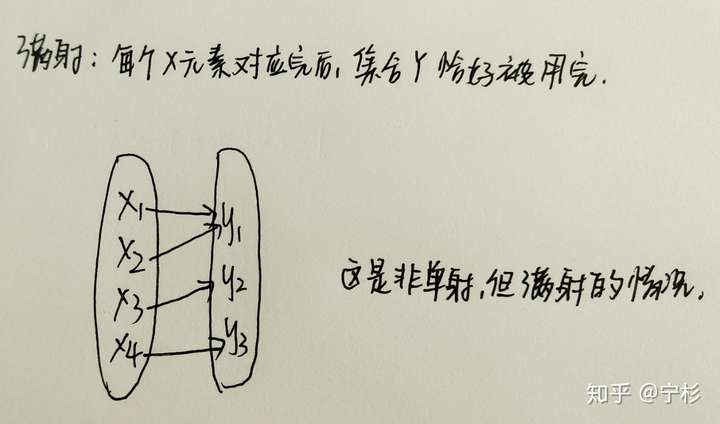
(3)一一映射,又称双射,即同时满足单射和满射。
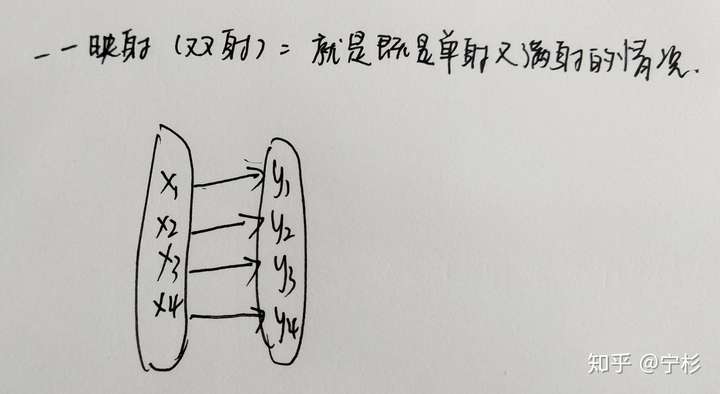
映射除了这三种情况,还延伸出了相关内容——逆映射和复合映射。
与我们之前接触的反函数相似,逆映射:



复合映射:
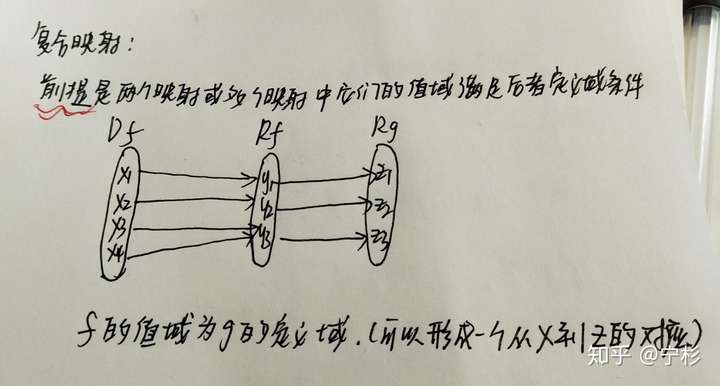
以上是关于映射的内容,下面我们来看看函数。
由于函数是映射的一种特殊情况,所以函数的本质也是一种对应关系。
介于我们高中是学过基本函数的,所以相信各位对函数的性质→奇偶性、单调性、以及周期性都是知道的,所以我就不讲这几个了,主要提一下函数的有界性。

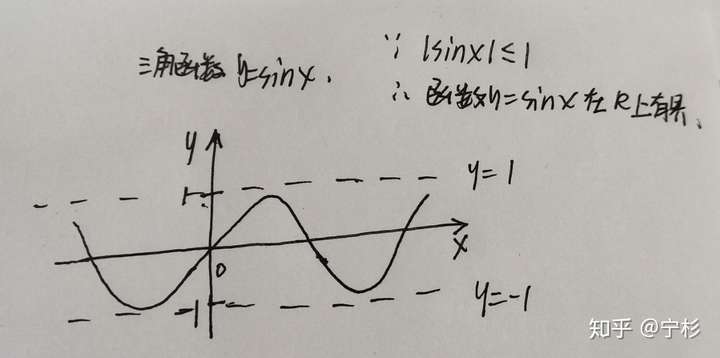
初等函数:经过有限次的四则运算和有限次的函数复合步骤所组成的可用一个式子表示的函数。
比如三角函数,它就是基本初等函数。
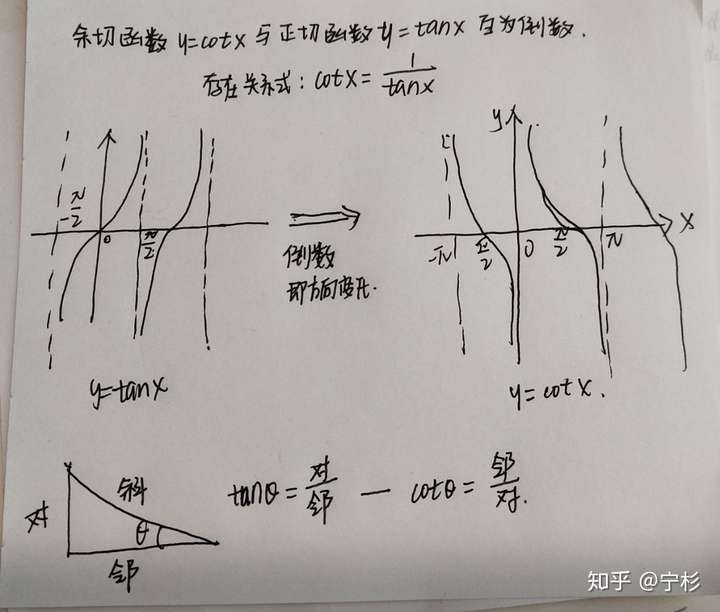 余切函数与正切函数
余切函数与正切函数
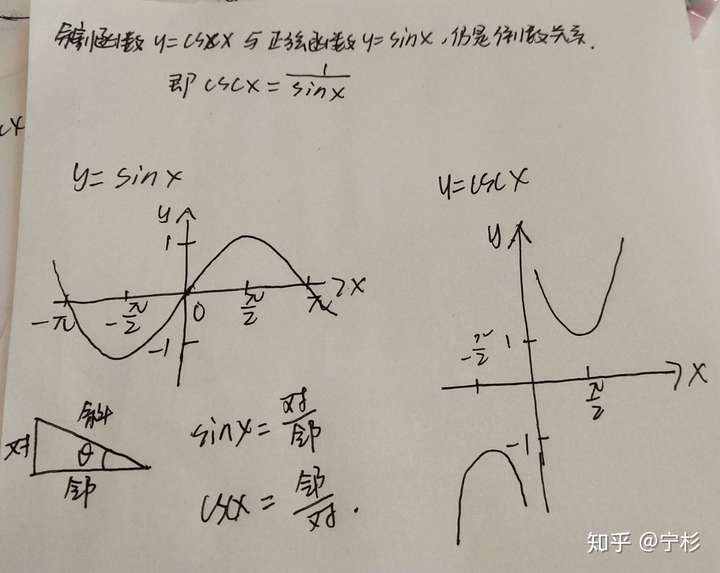 余割函数与正弦函数
余割函数与正弦函数
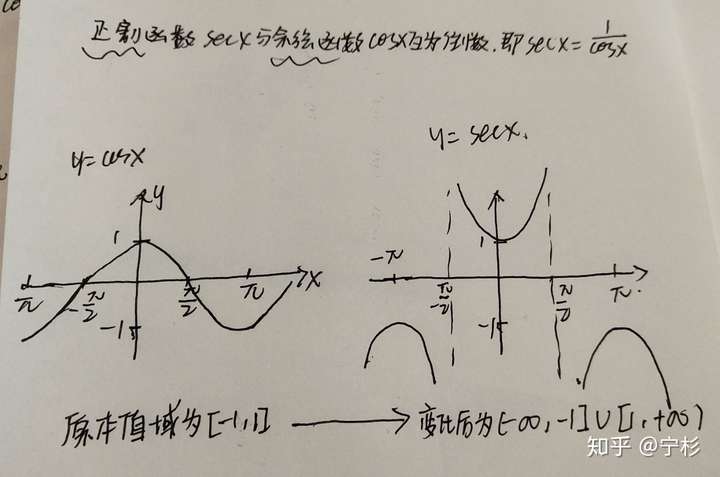 正割函数与余弦函数
正割函数与余弦函数