1.异常值分析
异常值是指样本中的个别值,其数值明显偏离其余的观测值。
异常值也称离群点,异常值的分析也称为离群点的分析。
异常值分析 → 3σ原则 / 箱型图分析
异常值处理方法 → 删除 / 修正填补
1.1 3σ原则 / 箱型图分析
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy import stats % matplotlib inline
# 异常值分析 # (1)3σ原则:如果数据服从正态分布,异常值被定义为一组测定值中与平均值的偏差超过3倍的值 → p(|x - μ| > 3σ) ≤ 0.003 data = pd.Series(np.random.randn(10000)*100) print(data.head()) # 创建数据 u = data.mean() # 计算均值 std = data.std() # 计算标准差 stats.kstest(data, 'norm', (u, std)) #正态分布的方式,得到 KstestResult(statistic=0.012627414595288711, pvalue=0.082417721086262413),P值>0.5 print('均值为:%.3f,标准差为:%.3f' % (u,std)) print('------') # 正态性检验
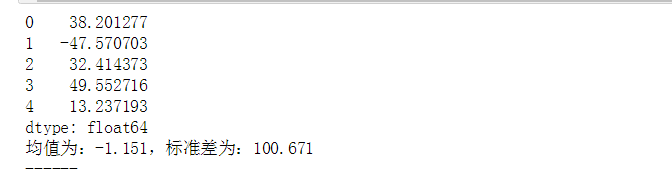
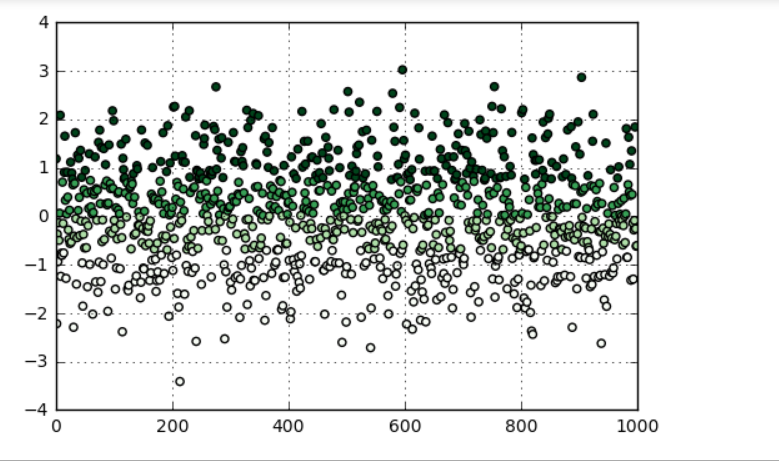
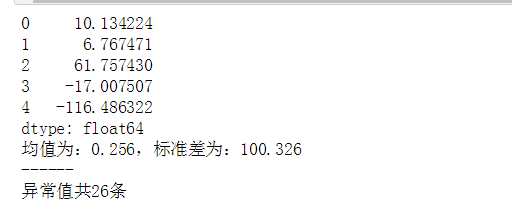
fig = plt.figure(figsize = (10,6)) ax1 = fig.add_subplot(2,1,1) data.plot(kind = 'kde',grid = True,style = '-k',title = '密度曲线') plt.axvline(3*std,hold=None,color='r',linestyle="--",alpha=0.8) #3倍的标准差 plt.axvline(-3*std,hold=None,color='r',linestyle="--",alpha=0.8) # 绘制数据密度曲线 error = data[np.abs(data - u) > 3*std] #超过3倍差的数据(即异常值)筛选出来 data_c = data[np.abs(data - u) < 3*std] print('异常值共%i条' % len(error)) ax2 = fig.add_subplot(2, 1, 2) plt.scatter(data_c.index, data_c, color = 'k', marker = '.', alpha = 0.3) plt.scatter(error.index, error, color = 'r', marker = '.', alpha = 0.7) plt.xlim([-10,10010]) plt.grid() # 图表表达

1.2箱型图分析
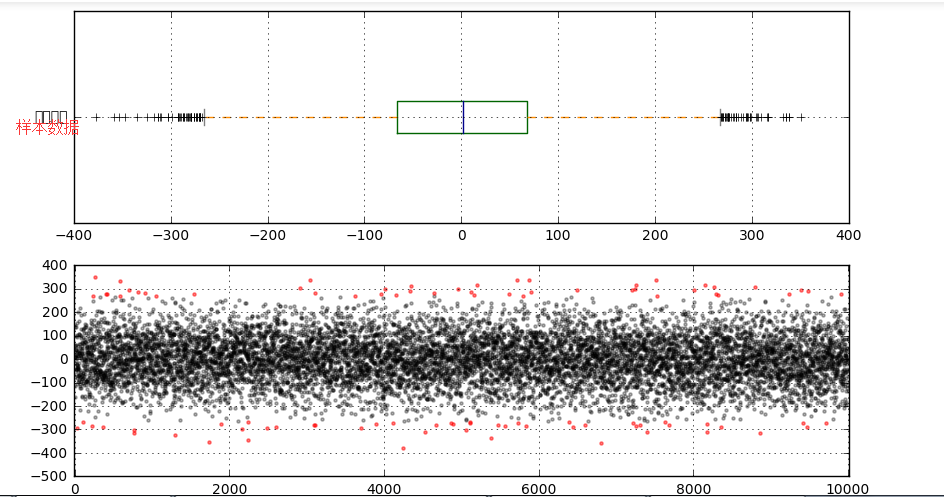
# 异常值分析 # (2)箱型图分析 fig = plt.figure(figsize = (10,6)) ax1 = fig.add_subplot(2,1,1) color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray') data.plot.box(vert=False, grid = True,color = color,ax = ax1,label = '样本数据') # 箱型图看数据分布情况 # 以内限为界
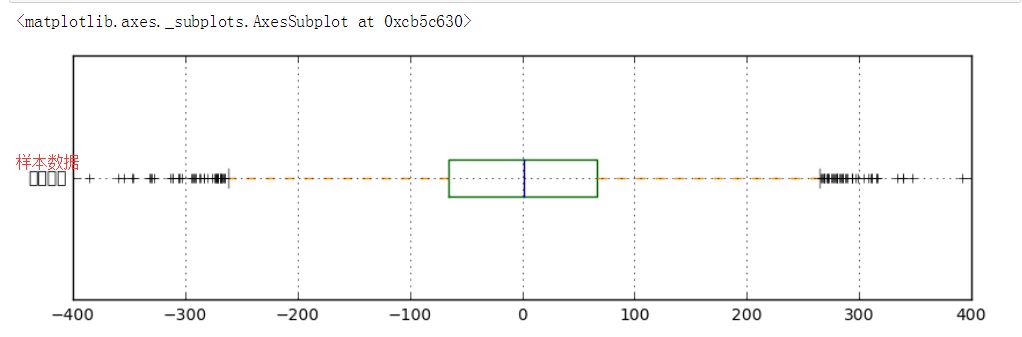
s = data.describe() print(s) print('------') # 基本统计量 q1 = s['25%'] q3 = s['75%'] iqr = q3 - q1 mi = q1 - 1.5*iqr ma = q3 + 1.5*iqr print('分位差为:%.3f,下限为:%.3f,上限为:%.3f' % (iqr,mi,ma)) print('------') # 计算分位差 ax2 = fig.add_subplot(2,1,2) error = data[(data < mi) | (data > ma)] data_c = data[(data >= mi) & (data <= ma)] print('异常值共%i条' % len(error)) # 筛选出异常值error、剔除异常值之后的数据data_c plt.scatter(data_c.index,data_c,color = 'k',marker='.',alpha = 0.3) plt.scatter(error.index,error,color = 'r',marker='.',alpha = 0.5) plt.xlim([-10,10010]) plt.grid() # 图表表达

2. 数据归一化
数据归一化/ 标准化
数据的标准化(normalization)是将数据按比例缩放,使之落入一个小的特定区间。
在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权
最典型的就是数据的归一化处理,即将数据统一映射到[0,1]区间上
0-1标准化 / Z-score标准化
(1)0 - 1标准化
将数据的最大最小值记录下来,并通过Max-Min作为基数(即Min=0,Max=1)进行数据的归一化处理
x = (x - Min) / (Max - Min)
import numpy as np import pandas as pd import matplotlib.pyplot as plt % matplotlib inline
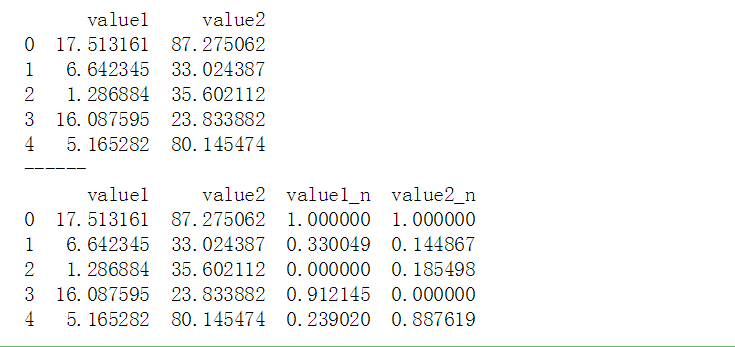
# 数据标准化 # (1)0-1标准化 df = pd.DataFrame({"value1":np.random.rand(10)*20, 'value2':np.random.rand(10)*100}) print(df.head()) print('------') # 创建数据 def data_norm(df,*cols): df_n = df.copy() for col in cols: ma = df_n[col].max() mi = df_n[col].min() df_n[col + '_n'] = (df_n[col] - mi) / (ma - mi) return(df_n) # 创建函数,标准化数据 df_n = data_norm(df, 'value1', 'value2') print(df_n.head())#标准化数据
(2)Z - score标准化
Z分数(z-score),是一个分数与平均数的差再除以标准差的过程 → z=(x-μ)/σ,其中x为某一具体分数,μ为平均数,σ为标准差
Z值的量代表着原始分数和母体平均值之间的距离,是以标准差为单位计算。在原始分数低于平均值时Z则为负数,反之则为正数
数学意义:一个给定分数距离平均数多少个标准差?
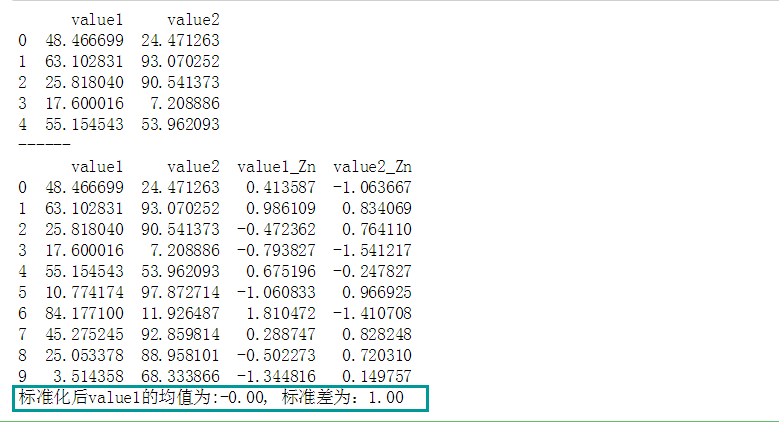
# 数据标准化 # (2)Z-score标准化 df = pd.DataFrame({"value1":np.random.rand(10) * 100, 'value2':np.random.rand(10) * 100}) print(df.head()) print('------') # 创建数据 def data_Znorm(df, *cols): df_n = df.copy() for col in cols: u = df_n[col].mean() std = df_n[col].std() df_n[col + '_Zn'] = (df_n[col] - u) / std #平均值/标准差 return(df_n) # 创建函数,标准化数据 df_z = data_Znorm(df,'value1','value2') u_z = df_z['value1_Zn'].mean() std_z = df_z['value1_Zn'].std() print(df_z) print('标准化后value1的均值为:%.2f, 标准差为:%.2f' % (u_z, std_z)) # 标准化数据 # 经过处理的数据符合标准正态分布,即均值为0,标准差为1 # 什么情况用Z-score标准化: # 在分类、聚类算法中,需要使用距离来度量相似性的时候,Z-score表现更好
案例应用
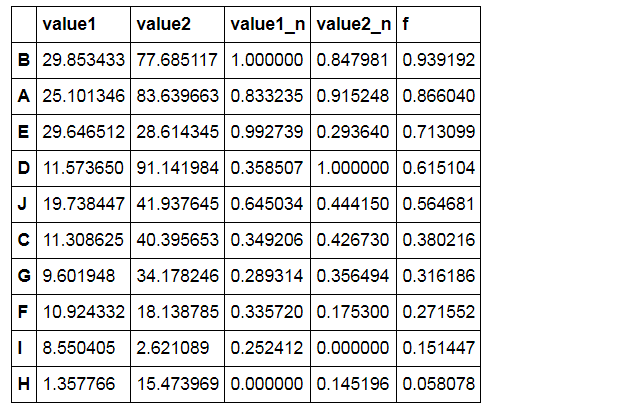
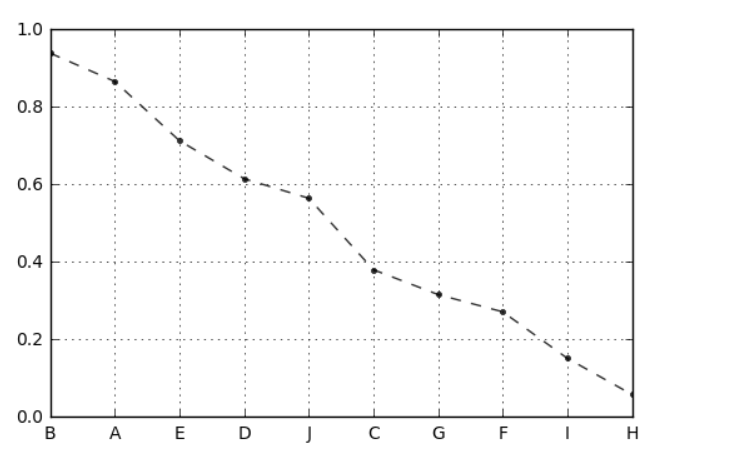
# 案例应用 # 八类产品的两个指标value1,value2,其中value1权重为0.6,value2权重为0.4 # 通过0-1标准化,判断哪个产品综合指标状况最好 df = pd.DataFrame({"value1":np.random.rand(10) * 30, 'value2':np.random.rand(10) * 100}, index = list('ABCDEFGHIJ')) #print(df.head()) #print('------') # 创建数据" df_n1 = data_norm(df,'value1','value2') # 进行标准化处理 df_n1['f'] = df_n1['value1_n'] * 0.6 + df_n1['value2_n'] * 0.4 df_n1.sort_values(by = 'f',inplace=True,ascending=False) df_n1['f'].plot(kind = 'line', style = '--.k', alpha = 0.8, grid = True) df_n1 # 查看综合指标状况
3.数据连续属性离散化
连续属性变换成分类属性,即连续属性离散化。
在数值的取值范围内设定若干个离散划分点,将取值范围划分为一些离散化的区间,最后用不同的符号或整数值代表每个子区间中的数据值
等宽法 / 等频法
(1)等宽法
将数据均匀划分成n等份,每份的间距相等
cut方法
import numpy as np import pandas as pd import matplotlib.pyplot as plt % matplotlib inline
# 等宽法 → cut方法 ages=[20,22,25,27,21,23,37,31,61,45,41,32] # 有一组人员年龄数据,希望将这些数据划分为“18到25”,“26到35”,“36到60”,“60以上”几个面元,分成4个区间。 bins = [18,25,35,60,100] cats = pd.cut(ages,bins) print(cats) print(type(cats)) print('---’) ## 返回的是一个特殊的Categorical类对象 → 一组表示面元名称的字符串

print(cats.codes, type(cats.codes)) # 0-3对应分组后的四个区间,用代号来注释数据对应区间,结果为ndarray;可以查看里边的等级 print(cats.categories, type(cats.categories)) # 四个区间,结果为index print(pd.value_counts(cats)) # 按照区间计数 print('-------') # cut结果含有一个表示不同分类名称的层级数组以及一个年龄数据进行标号的代号属性

print(pd.cut(ages,[18,26,36,61,100],right=False)) print('-------') # 通过right函数修改闭端,默认为True group_names=['Youth','YoungAdult','MiddleAged','Senior'] print(pd.cut(ages,bins,labels=group_names)) print('-------') # 可以设置自己的区间名称,用labels参数

df = pd.DataFrame({'ages':ages})
group_names=['Youth','YoungAdult','MiddleAged','Senior']
s = pd.cut(df['ages'],bins) # 也可以 pd.cut(df['ages'],5),将数据等分为5份
df['label'] = s
cut_counts = s.value_counts(sort=False)
print(df)
print(cut_counts)
# 对一个Dataframe数据进行离散化,并计算各个区间的数据计数
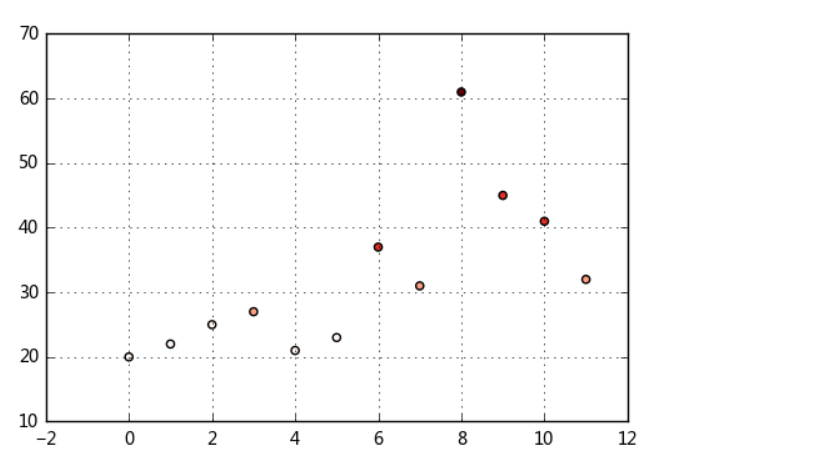
plt.scatter(df.index,df['ages'],cmap = 'Reds',c = cats.codes)
plt.grid()
# 用散点图表示,其中颜色按照codes分类
# 注意codes是来自于Categorical对象

(2)等频法
以相同数量的记录放进每个区间
qcut方法
# 等频法 → qcut方法 data = np.random.randn(1000) s = pd.Series(data) cats = pd.qcut(s,4) # 按四分位数进行切割,可以试试 pd.qcut(data,10) print(cats.head()) print(pd.value_counts(cats)) print('------') # qcut → 根据样本分位数对数据进行面元划分,得到大小基本相等的面元,但并不能保证每个面元含有相同数据个数 # 也可以设置自定义的分位数(0到1之间的数值,包含端点) → pd.qcut(data1,[0,0.1,0.5,0.9,1]) plt.scatter(s.index,s,cmap = 'Greens',c = pd.qcut(data,4).codes) plt.xlim([0,1000]) plt.grid() # 用散点图表示,其中颜色按照codes分类 # 注意codes是来自于Categorical对象