最大密度子图

最大密度子图

参考

胡伯涛论文

博客总结

无向图 (G(V,E)) 的密度 (D = dfrac {|E|} {|V|})

若选择了边 ((u,v)) 则必须有 (u in V , v in V)

最大密度子图

具有最大密度的子图，最大化 (D' = dfrac {|E'|} {|V'|})

根据之前的分数规划

可以二分答案

并且有如下引理

• 任意两个子图的密度差 (ge dfrac 1{n^2})

(dfrac {m_1}{n_1} - dfrac {m_2}{n_2} = dfrac {m_1n_2 - m_2n_1} {n_1n_2} ge dfrac 1 {n_1n_2} ge dfrac 1 {n^2})

现在的主要问题是如何 (Judge)

设要检验的值为 (g) , 构造函数 $f = |E| - g|V| $ , 现在的目标是使得 (f) 最大

有两种方法

1. 最大权闭合子图

目标：

最大化 (f = |E| - g|V|)

把无向边 ((u,v)) 看做一个点连接两条有向边指向 (u) 和 (v) 原图的点权值设为 (-g) ，

边的点为 (1) ,这样就转成了最大权闭合子图的问题

2.优化算法（诱导子图最小割）

对于点集 (V') , 显然能选的边要尽可能的都选上

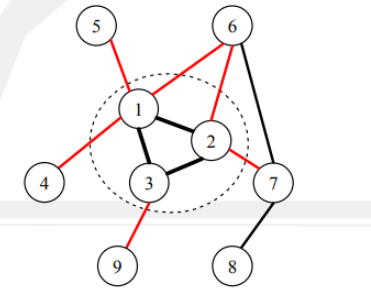
所有能选的边为 (V') 中点的度的和减去割 ([V',overline{V'}]) 的容量的一半

[|E'| = dfrac {sum_{vin V'}deg(v) -c[V',overline{V'}]}2 ]

[f = dfrac 12ig(sum_{vin V'}deg(v)-c[V',overline{V'}] - 2sum_{v in V'}gig) \ = dfrac 12ig(sum_{vin V'}(deg(v)-2g)-c[V',overline{V'}] ig) ]

按如下建图, (U) 是一个大常数，保证边权不是负数

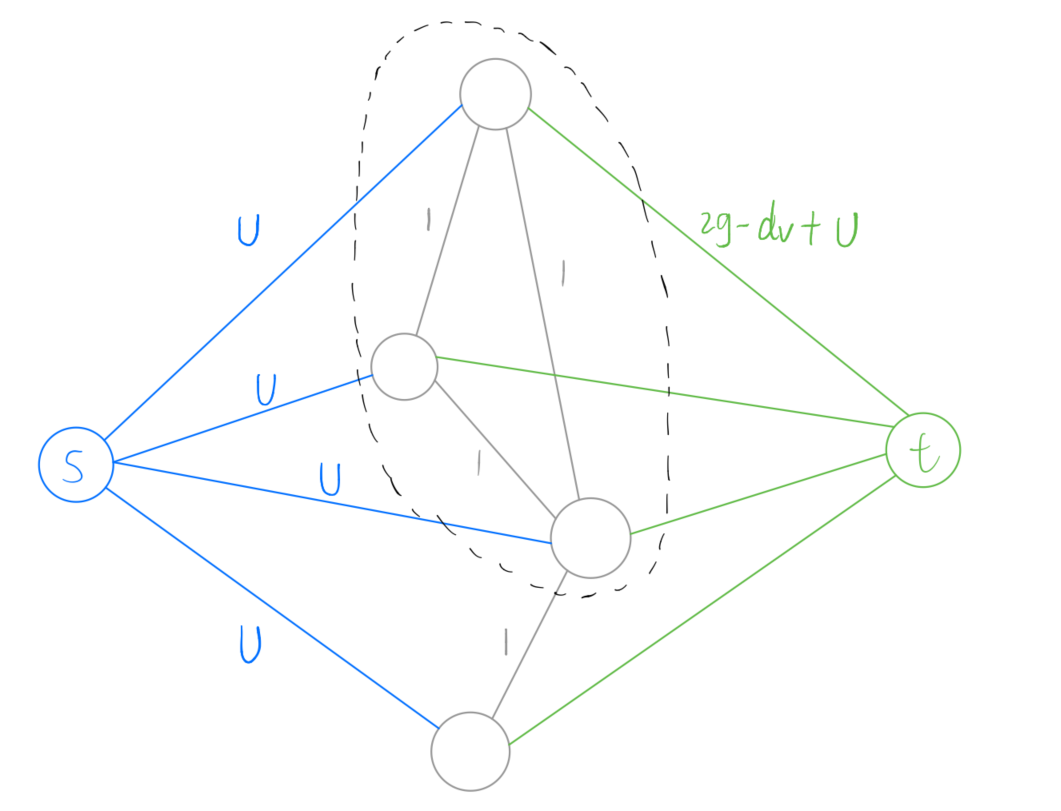
割 ([S,T]) , (S = {s} + V') ,(T = {t} + overline{V'})

割的容量 (c[S,T]) 有四个部分

(s o t) ： (0)

(s o overline{V'}) : (sum_{v in overline{V'}}U)

(V' o overline{V'}) ： 其实就是 (c[V',overline{V'}])

(V' o t) ： (sum_{vin V'}U+2g-d_v)

[c[S,T] = c[V',overline{V'}] + Un + sum_{v in V'}2g-d_v = Un -2f ]

所以最大化 (f) 即最小化 (c[S,T]) ，求最小割就可以了