统计和概率的关系:
重要的统计量:
- 期望

- 方差

- 协方差

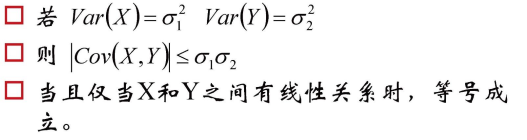

- 相关系数

- 独立和不相关
 从而有下面:
从而有下面:

独立性是指两个变量的发生概率一点关系没有,而相关性通常是指线性关系。如果两个变量不相关,指的是线性关系里不相关,但是不能说它们没
有关系,可能是线性以外的其他关系。
- 协方差矩阵
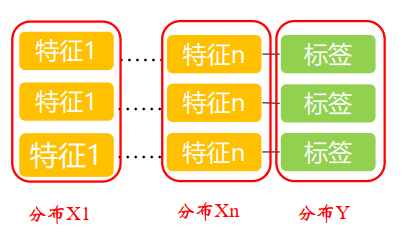
类似上图中,X1、X2、X3、、、Xn都是列向量,表示整个数据集中一个“特性”的数据,放在一个列向量中,则上图中的特性矩阵可以表示为X={X1、X2、X3、、、Xn}
则其中任意的一对Xi和Xj都可以求一次协方差,而这些协方差组成的矩阵就是协方差矩阵。如下:

协方差矩阵是一个对称矩阵,这矩阵中的每一项Cij表示Xi和Xj的两个特征的协方差,如果Cij等于0表示这两个特征不相关(这里指线性相关,当在二
维中两个变量不相关则可以得出这两个变量独立),两个变量不相关并不一定表示这两个变量相互独立,有可能是在其他高维相关或者非线性相关。
- 矩
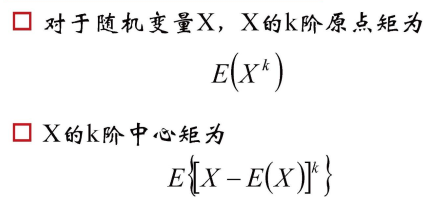
- 统计参数的总结

重要的定理和不等式:
- Jensen不等式

- 切比雪夫不等式

- 大数定理


该重要的推论叫做伯努利定理,这也是最找到的大数定理的形式。该定理表明事件A发生的频率Na/N依概率收敛于事件A的概率P。
- 中心极限定理

用样本估计参数
- 矩估计
- 极大似然估计