集合
1.定义:
由不同元素组成的集合,集合中是一组无序排列的可hash值,可以作为字典的key
2.创建格式:
可以使用大括号 set() 函数创建集合
注意:创建一个空集合必须用{ },因为 set_1={1,2,3}
set_2=set([1,2,3])
set_3=set() #空集合
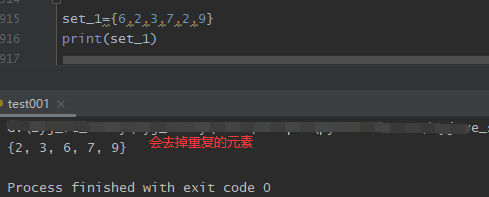
3.集合具有去重的功能
集合中的元素都具有唯一性,所以集合具有去重功能
4、添加元素
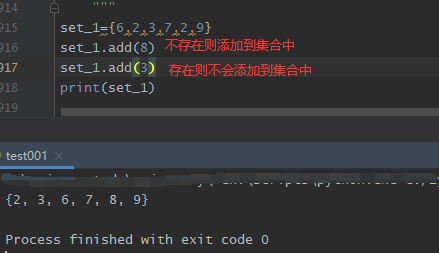
1.set.add(x),x是一个可hash的对象
将元素 x 添加到集合 中,如果元素已存在,则不进行任何操作。
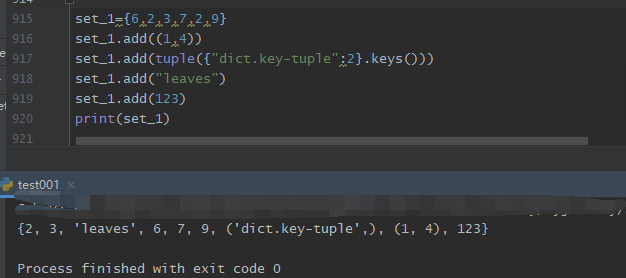
如果元素的元组,字符串,数字等不可改变的数据类型,则会在集合中以元组,字符串,数字的形式添加到集合中,成为集合的一个元素
2.s.update(x),x是一个可迭代的对象
还有一个方法,也可以添加元素,且参数可以是列表,元组,字典,字符串等,语法格式如下:
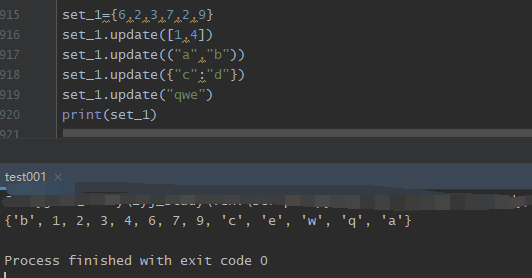
5.移除元素:
1. set.remove(x)
将元素 x 从集合 s 中移除,如果元素不存在,则会发生错误。
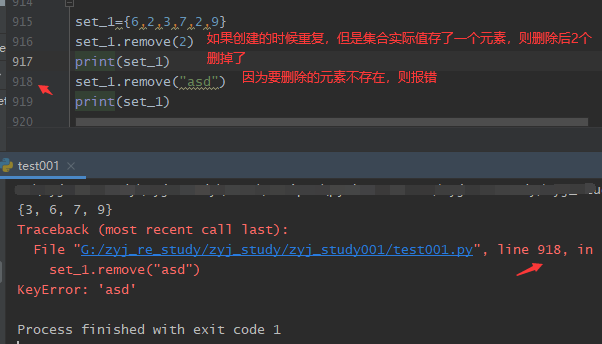
2. s.discard( x )
移除集合中的元素,且如果元素不存在,不会发生错误。格式如下所示:
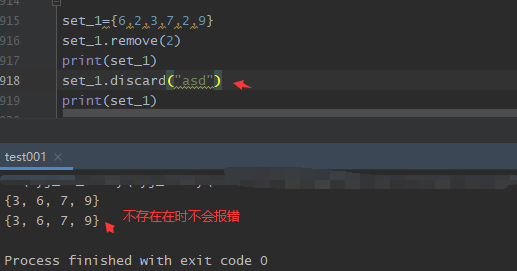
3. set.pop()
set 集合的 pop 方法会对集合进行无序的排列,然后将这个无序排列集合的左面第一个元素进行删除
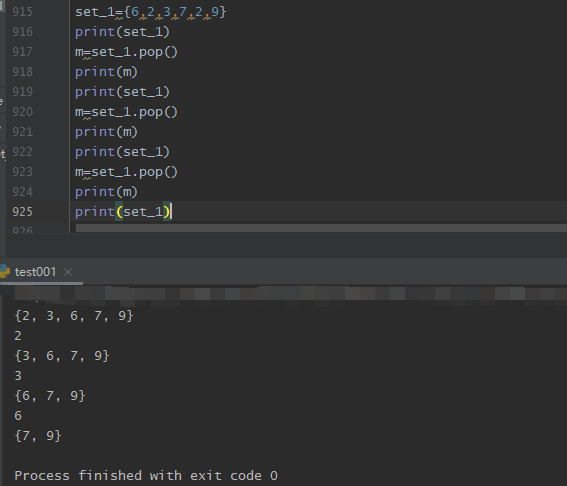
4. 清空集合 s.clear()
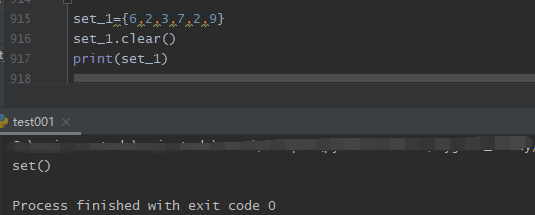
5. 删除集合对象(del set)
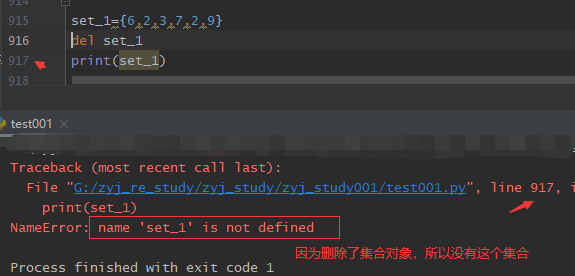
6.集合的基本运算
1.并集:
由所有属于集合A或者是属于集合B的元素组成的集合,称为集合A与B的并集,记作A∪B,即A∪B={x|x∈A或x∈B},用Veen图表示为
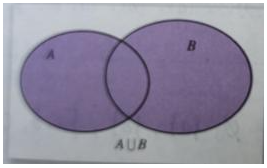
集合a或b中包含的所有元素
1. set_1 | set_2
2. set_1.union(set_2)
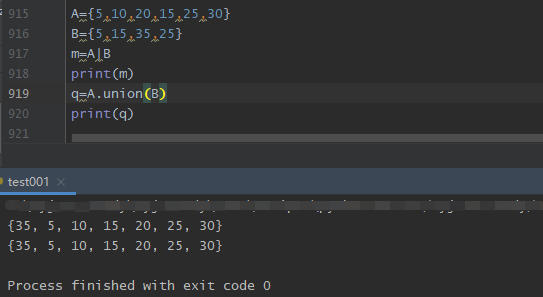
2.交集:
一般地,由属于集合A并且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B,
即A∩B={x|x∈A且x∈B},用Veen 图表示为
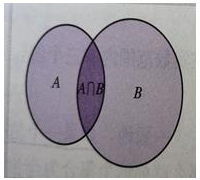
集合a或b中包含的所有元素
1. set_1 & set_2
2.set_1.instersection(set_2)
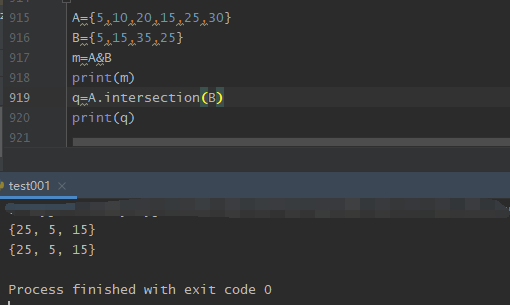
3.补集:
全集:一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记作U
补集:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合就称为集合A相对于全集U的补集,简称为集合A的补集,记作CuA,即 CuA={x|x∈U且x∉A},用Veen图表示为
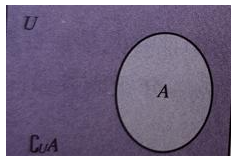
不同时包含于a和b的元素
1. a ^ b
2. set_1.symmetric_difference(set_2)
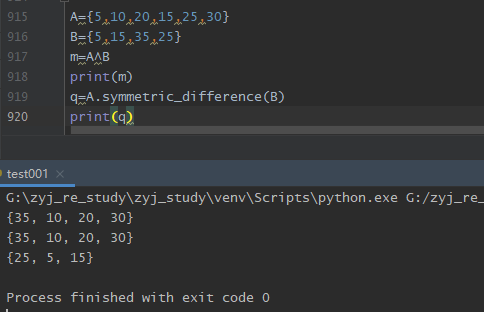
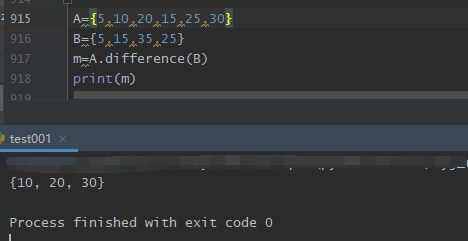
4.差集:
记A,B是两个集合,则所有属于A且不属于B的元素构成的集合,叫做集合A减集合B(或集合A与集合B之差),类似地,对于集合A、B,把集合{x∣x∈A,且x∉B}叫做A与B的差集。
记作:B-A
差集--集合a中包含而集合b中不包含的元素
1. set_1 - set_2
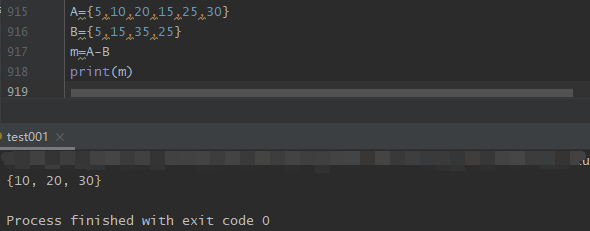
2. set.difference(set)