很久之前写的学习笔记,就搬过来了
Q:线段树是什么?
A:一种数据结构,支持(O(log(N)))修改和查询区间,所以在(N)的序列(M)次查询下,复杂度只有(O(Mlog(N))),相比起朴素算法的(O(N))查询和修改,优秀的很多。
那么怎么实现呢?
我们不妨考虑一种下面这样的结构
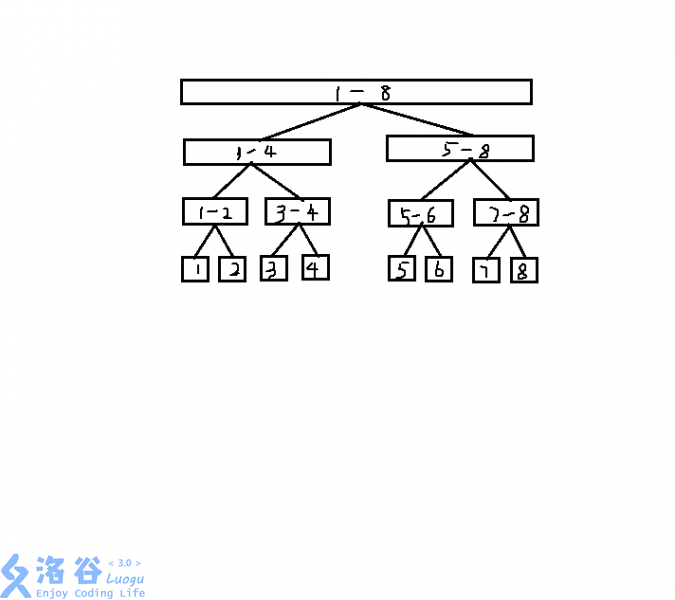
怎么样,是不是很像一棵完全二叉树,这样子不难看出复杂度是(O(log(N)))级别的,但是要注意的一点是,线段树的数组一定要开到(4N)!
建树
对于这个题而言,我们用(su[4N])数组来维护区间的和,那么此线段树可以通过递归的到,即(build(k*2,l,mid))取得左儿子,(build(k*2+1,mid+1,r))取得右儿子,当(l=r)时(su)便等于当前值(a[l])。代码如下
ll build(ll k,ll l,ll r)
{
if (l==r)
{
su[k]=a[l];
return 0;
}
ll mid=(l+r)>>1;
build(k*2,l,mid);
build(k*2+1,mid+1,r);
su[k]=su[k*2]+su[k*2+1];
}
区间加
如果说直接将v加到su里,那么肯定会tle,所以我们考虑用一个标记,即Lazy Tag,当要对区间([x,y])进行加法,那么我们给这段区间打上标记,(add[k]=v),在之后的询问和修改中再把标记进行下放,这样子的复杂的仍然是(O(log(N)))。代码如下
ll add(ll k,ll l,ll r,ll v) //打标记
{
ad[k]+=v;
su[k]+=(r-l+1)*v;
}
ll pd(ll k,ll l,ll r,ll mid) //下放标记
{
if (!ad[k])return 0;
add(k*2,l,mid,ad[k]);
add(k*2+1,mid+1,r,ad[k]);
ad[k]=0;
}
ll change(ll k,ll l,ll r,ll x,ll y,ll v) //区间加
{
if (l>=x&&r<=y)return add(k,l,r,v);
ll mid=(l+r)>>1;
pd(k,l,r,mid);
if (x<=mid)change(k*2,l,mid,x,y,v);
if (mid<y)change(k*2+1,mid+1,r,x,y,v);
su[k]=su[k*2]+su[k*2+1];
}
区间询问和
这个就变得非常简单了,只要分别递归有关x和y的区间,加起来即可。注意在询问时也要下放标记。 代码如下
ll que(ll k,ll l,ll r,ll x,ll y)
{
if (l>=x&&r<=y)return su[k];
ll mid=(l+r)>>1,res=0;
pd(k,l,r,mid);
if (x<=mid)res+=que(k*2,l,mid,x,y);
if (mid<y)res+=que(k*2+1,mid+1,r,x,y);
return res;
}
区间乘
既然多了乘法,我们肯定就要再开一个(LazyTag:mu[4*N]),开始时一定要初始化为1!,而和加法的(LazyTag)不同的是在改变乘法(LazyTag)时,也要改变加法的(LazyTag),即
ll mul(ll k,ll l,ll r,ll v)
{
mu[k]=(mu[k]*v)%p;
ad[k]=(ad[k]*v)%p;
su[k]=(su[k]*v)%p;
}
然后我们再考虑(pushdown)操作,假如一个序列([1,3,5,9,12]),先在([2,4])区间加上一个数(k),序列变为([1,3+k,5+k,9+k,12]),然后在([3,5])区间乘上一个数(r),序列变为([1,3+k,(5+k)*r,(9+k)*r,12*r]),
由此看出,我们如果先(pushdown)加法,再(pushdown)乘法,会导致之前的加法也被乘一次,也就是((a+b)*c)但(b)并不需要(*c),也就是我们想要(a*c+b),所以就要先(pushdown)乘法,再(pushdown)加法,即
pudn(k,l,r,mid);//乘法
pd(k,l,r,mid);//加法