Apple Tree 有时间戳的树状数组

Problem Description

There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

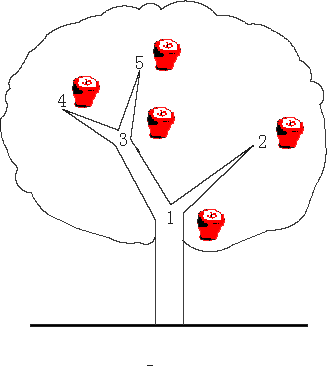
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

 

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

 

Output

For every inquiry, output the correspond answer per line.

 

Sample Input

3 1 2 1 3 3 Q 1 C 2 Q 1

 

Sample Output

3 2

**********************************************************************************************************************************

最重要的是记录树状数组的时间戳

**********************************************************************************************************************************

/*
 有时间戳的树状数组，
*/
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<queue>
#include<cstdio>
#include<map>
#include<algorithm>
using namespace std;
#define  maxn  220000
typedef vector<int> VCT_INT;
vector<VCT_INT>G(maxn/2);
int nCount,n,m;
int Start[maxn],End[maxn];
int C[maxn],lowbit[maxn];
int HasApple[maxn/2];
 int query_sum(int p)//求一个区间内的和
 {
    int sum=0;
    while(p>0)
    {
       sum+=C[p];
       p-=lowbit[p];
    }
    return sum;
 }

 void modify(int p,int val)//插入更新
 {
     while(p<=nCount)
     {
        C[p]+=val;
        p+=lowbit[p];
     }
 }

void dfs(int s)//插入时间戳
{
   Start[s]=++nCount;
   for(int it=0;it<G[s].size();it++)
    {
       dfs(G[s][it]);
    }
    End[s]=++nCount;
}

int main()
{
   int i,j,k;
   while(scanf("%d",&n)!=EOF)
   {
      int a,b,c;
     for(i=1;i<n;i++)
     {
        scanf("%d %d",&a,&b);
        G[a].push_back(b);
     }
     nCount=0;
     dfs(1);
     for(i=1;i<=nCount;i++)
      lowbit[i]=i&(i^(i-1));
     for(i=1;i<=nCount;i++)//求C[]数组
      C[i]=i-(i-lowbit[i]+1)+1;
     for(i=1;i<=n;i++)
     {
       HasApple[i]=1;
     }
      scanf("%d",&m);
    for(i=0;i<m;i++)
    {
        char cmd[10];
        int a;
        scanf("%s%d",cmd,&a);
        if(cmd[0]=='C')
        {
            if(HasApple[a])
            {
                modify(Start[a],-1);
                modify(End[a],-1);
                HasApple[a]=0;
            }
            else
            {
                modify(Start[a],1);
                modify(End[a],1);
                HasApple[a]=1;
            }
        }
        else
        {
            int t1=query_sum(End[a]);
            int t2=query_sum(Start[a]);
            printf("%d
",(t1-t2)/2+HasApple[a]);
        }
    }
   }
}