Description
天平的两边有时不一定只能挂物品,还可以继续挂着另一个天平,现在给你一些天平的情况和他们之间的连接关系,要求使得所有天平都能平衡所需物品的总重量最轻,一个天平平衡当且仅当“左端点的重量*左端点到支点的距离=右端点的重量*右端点到支点的距离”。注意题目中的输入保证这些天平构成一个整体。
Input
第一行包含一个N(N<=100),表示天平的数量,,天平编号为1到N,接下来包含N行描述天平的情况,每行4个整数P,Q,R,B,P和Q表示横杆上支点到左边的长度与到右边的距离的比例为P:Q,R表示左边悬挂的情况,如果R=0说明悬挂的物品,否则表示左边悬挂的是天平R;B表示右边的悬挂情况,如果B=0表示右边悬挂的是物品,否则右边悬挂着天平B。
对于所有的输入,保证W*L<2^31,其中W为最轻的物品重量,而L为输入中描述左右比例时出现的最大值。
对于所有的输入,保证W*L<2^31,其中W为最轻的物品重量,而L为输入中描述左右比例时出现的最大值。
Output
输出一个整数表示使得所有天平都平衡所需最轻的物品总重量。
Sample Input
4
3 2 0 4
1 3 0 0
4 4 2 1
2 2 0 0
Sample Output
40
Hint

如果我们一个天平的两边的所有天平都平衡了,现在我们要调平这个天平。
假设重量是W1,W2,左右两臂长度是L1,L2,我们要把第一个重量放大X倍,第二个放大Y倍
则明显我们就有X*W1*L1=Y*W2*L2
现在我们肯定要求X与Y的最小比值才能保证所有的重量是最小的
我们显然有式子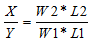
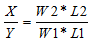
显然我们要求比值就可以求W2*L2与W1*L1的最大公约数,X=W2*L2/gcd,Y=W1*L1/gcd
然后递归回去就可以了
如果我们遇到空节点就直接返回1,显然
注意1号杠杆并不一定是最上面的杠杆,所以我们要记录一下父亲关系找到最上面的杆子
code:
1 #include<iostream> 2 #include<cstdio> 3 #define N 100006 4 using namespace std; 5 int gcd(int a,int b){ 6 if(a<b)swap(a,b); 7 while(a=a%b)swap(a,b); 8 return b; 9 } 10 int lcm(int a,int b){ 11 return a/gcd(a,b)*b; 12 } 13 struct node{ 14 int P,Q,L,R,W; 15 }e[N]; 16 int dfs(int x){ 17 if(x==0)return 1; 18 int left=dfs(e[x].L),right=dfs(e[x].R); 19 int p=gcd(e[x].P*left,e[x].Q*right); 20 int X=e[x].P*left/p,Y=e[x].Q*right/p; 21 return X*right+Y*left; 22 } 23 int fa[N]; 24 int main(){ 25 int n; 26 cin>>n; 27 for(int i=1;i<=n;i++)fa[i]=i; 28 for(int i=1;i<=n;i++){ 29 int P,Q,L,R; 30 cin>>e[i].P>>e[i].Q>>e[i].L>>e[i].R; 31 fa[e[i].L]=i,fa[e[i].R]=i; 32 } 33 int root=0; 34 while(fa[root]!=root){ 35 root=fa[root]; 36 } 37 cout<<dfs(root); 38 return 0; 39 }
over