在暴力的角度来说,如果我们$O(n)$枚举根节点,有没有办法在$O(n)$的时间内找到答案呢?
此时如果用树形$dp$的想法,发现是可做的,因为可以推得以下的结论:
设$x$为根节点,$d[i]$为$i$节点到$x$的距离(即深度),$g[i]$为$i$节点到最近的出入口(即叶子节点)的距离,$ans_{x}$为以$x$为根节点时的答案。
如果$d[i] geq g[i]$,则我们可以确定,以$i$为子树,对于$x$为根时的答案贡献为$1$。
如下图:
在对于以$i$为根的子树,会对$ans_{x}$产生$1$的贡献,可以理解为一个人从$i$为根的子树的任意叶子节点出发,可以比贝茜更先到达$i$
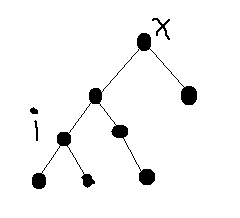
而这种解法只需要先$dfs$两次得到$g[i]$和$d[i]$,然后一次$dfs$得到答案,复杂度为$O(n^{2})$。
但是这种做法不够理想,我们还想更快的实现。
如果我们对树的性质较为熟悉,我们知道:
$1$.对于树的某棵子树,子树有m个节点,有:$sum du[i]=2*m-1$
$2$.对于某棵树,树有n个节点,有:$sum du[i]=2*n-2$
$PS$:$du[i]$为$i$节点的度。
将性质$1$变形为:$1=sum (2-du[i])$
在本题中,贡献为1的子树有一个性质,即:$d[i] geq g[i]& &d[fa[i]]<g[fa[i]]$。可以理解为他的父亲贡献为子节点个数,即上图中的$i$的父亲。
所以$ans_{x}$=贡献为1的子树数量之和。这不是废话吗......
所以根据性质$1$,有:$ans_{x}=sum_{i=1}^{n}[d[i] geq g[i]](2-du[i])$,稍微解释一下式子的来由:
因为子树的$sum (2-du[i])=1$,而$1$刚好是一颗子树的贡献,所以满足$d[i] geq g[i]$的点集,可以组成$ans_{x}$那么多棵贡献为1的子树。如下图:

所以满足$g[i] geq d[i]$的点集为上图圈出来的点,而答案为贡献为1的子树数量:$3$。
此时我们可以用点分治的想法,将:
$ans_{x}=sum_{i=1}^{n}[d[i] geq g[i]](2-du[i])$
求解问题变化成求解点对问题:
$ans_{x}=sum_{i=1}^{n}[dis(x,i) geq g[i]](2-du[i])$,$dis(x,i)$为$x$到$i$的距离。
所以设$w$为当前子树的重心,$p[i]$为$i$到重心的距离。
则$dis(x,i) geq g[i] ightarrow p[x]+p[i] geq g[i] ightarrow p[x] geq g[i]-p[i]$
而在每次求出$p[i]$后,可以使用树状数组维护$g[i]-p[i]$,不过注意$g[i]-p[i]$会小于0,所以维护时向右移$n$的数量。
细节问题可以看代码,其余的问题欢迎提问。
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1e5 + 5e4; 5 const int inf = 2e9 + 10; 6 struct node { 7 int s, e, w, next; 8 }edge[maxn]; 9 int head[maxn], len; 10 void init() { 11 memset(head, -1, sizeof(head)); 12 len = 0; 13 } 14 void add(int s, int e) { 15 edge[len].s = s; 16 edge[len].e = e; 17 edge[len].next = head[s]; 18 head[s] = len++; 19 } 20 int root, lens, sum; 21 int d[maxn], du[maxn], o[maxn], vis[maxn], g[maxn], son[maxn], siz[maxn], ans[maxn]; 22 int rt[maxn], n; 23 int lowbit(int x) { 24 return x & -x; 25 } 26 void Add(int x, int val) { 27 for (int i = x; i <= 2 * n; i += lowbit(i)) 28 rt[i] += val; 29 } 30 int query(int x) { 31 int ans = 0; 32 for (int i = x; i > 0; i -= lowbit(i)) 33 ans += rt[i]; 34 return ans; 35 } 36 void getroot(int x, int fa) { 37 siz[x] = 1, son[x] = 0; 38 for (int i = head[x]; i != -1; i = edge[i].next) { 39 int y = edge[i].e; 40 if (y == fa || vis[y])continue; 41 getroot(y, x); 42 siz[x] += siz[y]; 43 son[x] = max(son[x], siz[y]); 44 } 45 son[x] = max(son[x], sum - siz[x]); 46 if (son[x] < son[root])root = x; 47 } 48 void getd(int x, int fa) { 49 o[++lens] = x; 50 for (int i = head[x]; i != -1; i = edge[i].next) { 51 int y = edge[i].e; 52 if (y == fa || vis[y])continue; 53 d[y] = d[x] + 1; 54 getd(y, x); 55 } 56 } 57 void cal(int x, int val, int add) { 58 lens = 0, d[x] = val; 59 getd(x, 0); 60 for (int i = 1; i <= lens; i++) 61 Add(g[o[i]] - d[o[i]] + n, 2 - du[o[i]]); 62 for (int i = 1; i <= lens; i++) 63 ans[o[i]] += add * query(d[o[i]] + n); 64 for (int i = 1; i <= lens; i++) 65 Add(g[o[i]] - d[o[i]] + n, du[o[i]] - 2); 66 } 67 void solve(int x) { 68 cal(x, 0, 1); 69 vis[x] = 1; 70 for (int i = head[x]; i != -1; i = edge[i].next) { 71 int y = edge[i].e; 72 if (vis[y])continue; 73 cal(y, 1, -1); 74 sum = siz[y]; 75 root = 0; 76 getroot(y, 0); 77 solve(root); 78 } 79 } 80 void dfs1(int x, int fa, int dep) { 81 g[x] = inf; 82 if (du[x] == 1)g[x] = 0; 83 for (int i = head[x]; i != -1; i = edge[i].next) { 84 int y = edge[i].e; 85 if (y == fa)continue; 86 dfs1(y, x, dep + 1); 87 g[x] = min(g[x], g[y] + 1); 89 } 90 } 91 void dfs2(int x, int fa) { 92 for (int i = head[x]; i != -1; i = edge[i].next) { 93 int y = edge[i].e; 94 if (y == fa)continue; 95 g[y] = min(g[y], g[x] + 1); 96 dfs2(y, x); 97 } 98 } 99 int main() { 100 scanf("%d", &n); 101 init(); 102 for (int i = 1, x, y; i < n; i++) { 103 scanf("%d%d", &x, &y); 104 add(x, y); 105 add(y, x); 106 du[x]++, du[y]++; 107 } 108 dfs1(1, 0, 1); 109 dfs2(1, 0); 110 son[0] = n, root = 0, sum = n, getroot(1, 0); 111 solve(root); 112 for (int i = 1; i <= n; i++) { 113 if (du[i] == 1)printf("1 "); 114 else printf("%d ", ans[i]); 115 } 116 }