https://vjudge.net/problem/UVA-12171
题目
某人设计雕塑,用的是很扯的方法:把一堆长方体拼起来。给出长方体的坐标和长宽高,求外表面积。因为要将这雕塑进行酸洗,需要知道$V_排$
输入长方体信息,输出外表面积和$V_排$
[0le 每个维度的坐标值le 500]
[0le长、宽、高 le500]
(不会描述了)
题解
有了紫书上的提示,还是写了两个小时……
离散化+bfs
将长方体出现的坐标都存入数组,然后排序,然后使用 unique 函数, unique 函数的返回值是指向末尾哨兵的迭代器(?),减去 begin 就可以得到剩下元素个数。
unique复杂度$O(数组原来元素个数)$,如果没有排序,那么 unique函数就没有效果(只会把与上一个元素相同的元素无视,把后面的元素移动到前面(覆盖),而不是像紫书那样说的重复元素移动到后面)
https://en.cppreference.com/w/cpp/algorithm/unique
将雕塑放进长宽高都大于500的容器里面,然后灌水,容器的体积减去水的体积就是$V_排$,水的内表面积就是雕塑的外表面积
如果水碰到了雕塑,那么就计算表面积……
三维也可以离散化,画个图可以看出来
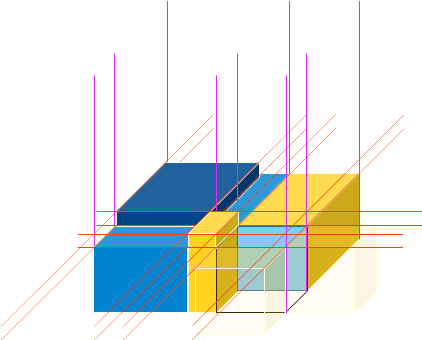
有个技巧是用左上角的坐标来代表长方体
计算面积的时候可以选择无视某条边
调试的时候可以使用文件输入……最好一开始先用简单的数据
BIG小于1000会WA……
(不想解释了= =)
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define REP(i,x,y) for(register int i=(x); i<(y); i++)
#define REPE(i,x,y) for(register int i=(x); i<=(y); i++)
#ifdef sahdsg
#define DBG(a,...) printf(a, ##__VA_ARGS__)
#else
#define DBG(a,...) (void)0
#endif
#define BIG 1008
template <class T>
inline void read(T& x) {
char c=getchar();int f=1;x=0;
while(!isdigit(c)&&c!='-')c=getchar();if(c=='-')f=-1,c=getchar();
while(isdigit(c)){x=x*10+c-'0';c=getchar();}x*=f;
}
struct _b {
int x_0, y_0, z_0;
int x_1, y_1, z_1;
} b[51];
int x[108], y[108], z[108];
int nx , ny , nz;
int cube[108][108][108];
int ans1=0, ans2=0;
struct node {
int x,y,z;
};
const int dx[] = { 0, 0,-1, 0, 0, 1};
const int dy[] = { 0,-1, 0, 0, 1, 0};
const int dz[] = {-1, 0, 0, 1, 0, 0};
void getans() {
ans1=0, ans2=BIG*BIG*BIG;
queue<node> q;
q.push((node){0,0,0});
cube[0][0][0]=2;
int delx=x[1]-x[0];
int dely=y[1]-y[0];
int delz=z[1]-z[0];
ans2-=delx*dely*delz;
while(!q.empty()) {
node now = q.front(); q.pop();
REP(i,0,6) {
int newx = now.x+dx[i], newy = now.y+dy[i], newz = now.z+dz[i];
if(newx<nx-1 && newx>=0)
if(newy<ny-1 && newy>=0)
if(newz<nz-1 && newz>=0) {
if(cube[newx][newy][newz]==0) {
q.push((node){newx,newy,newz});
cube[newx][newy][newz]=2;
int delx=x[newx+1]-x[newx];
int dely=y[newy+1]-y[newy];
int delz=z[newz+1]-z[newz];
// DBG("```%d %d %d
", delx, dely, delz);
ans2-=delx*dely*delz;
} else if(cube[newx][newy][newz]==1) {
int delx=dx[i]?1:(x[newx+1]-x[newx]);
int dely=dy[i]?1:(y[newy+1]-y[newy]);
int delz=dz[i]?1:(z[newz+1]-z[newz]);
ans1+=delx*dely*delz;
}
}
}
}
}
int main() {
#ifdef sahdsg
freopen("in.txt","r",stdin);
#endif
int T; scanf("%d", &T);
while(0<T--) {
int n; scanf("%d", &n);
REP(i,0,n) {
read(b[i].x_0); read(b[i].y_0); read(b[i].z_0);
read(b[i].x_1); read(b[i].y_1); read(b[i].z_1);
b[i].x_1+=b[i].x_0;
b[i].y_1+=b[i].y_0;
b[i].z_1+=b[i].z_0;
#define op(k) k[i*2]=b[i].k##_0; k[i*2+1]=b[i].k##_1;
op(x);op(y);op(z);
#undef op
}
x[2*n]=BIG-1;y[2*n]=BIG-1;z[2*n]=BIG-1;
x[2*n+1]=-1;y[2*n+1]=-1;z[2*n+1]=-1;
sort(x,x+2*n+2); sort(y,y+2*n+2); sort(z,z+2*n+2);
nx = unique(x,x+2*n+2)-x;
ny = unique(y,y+2*n+2)-y;
nz = unique(z,z+2*n+2)-z;
memset(cube,0,sizeof cube);
// REP(i,0,nx) REP(j,0,ny) REP(k,0,nz) DBG("```%d %d %d
", x[i], y[j], z[k]);
REP(i,0,n) {
#define op(k)
b[i].k##_0=lower_bound(k, k+n##k, b[i].k##_0)-k;
b[i].k##_1=lower_bound(k, k+n##k, b[i].k##_1)-k;
op(x);op(y);op(z);
#undef op
// DBG("%d %d
%d %d
%d %d
", b[i].x_0,b[i].x_1,b[i].y_0,b[i].y_1,b[i].z_0,b[i].z_1);
REP(qx,b[i].x_0,b[i].x_1) REP(qy,b[i].y_0,b[i].y_1) REP(qz,b[i].z_0,b[i].z_1) {
cube[qx][qy][qz]=1;
}
}
getans();
printf("%d %d
", ans1, ans2);
}
return 0;
}