UVA 11809 Floating-Point Numbers

题目链接：https://vjudge.net/problem/UVA-11809

题目翻译摘自《算法禁赛入门经典》

题目大意

　　计算机常用阶码-尾数的方法保存浮点数。如图所示，如果阶码有 6 位，尾数有 8 位， 可以表达的最大浮点数为$0.111111111_2 * 2^{111111_2}$。注意小数点后第一位必须为 1，所以一共有 9 位小数。 

　　

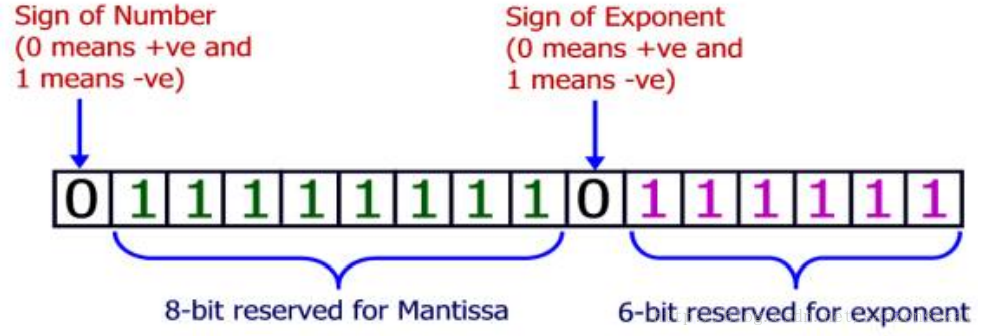
　　这个数换算成十进制之后就是$0.998046875 * 2^{63} = 9.205357638345294 * 10^{18}$。你的任务是根据这个最大浮点数，求出阶码的位数 E 和尾数的位数 M。输入格式为 AeB，表示最大浮点数为$A * 10^B$。$0 < A < 10$，并且恰好包含 15 位有效数字。输入结束标志为 0e0。对于每组数据，输出 M 和 E。输入保证有唯一解，且$0 leq M leq 9，1 leq E leq 30$。在本题中，M + E + 2 不必为 8 的整数倍。

分析

　　设最大值为 v，则$v = (1 - frac{1}{2^{M + 1}}) * 2^{2^E - 1} = A * 10^B$。

　　两边求以 10 为底的对数可得$lg v = lg (2^{M + 1} - 1) - (M + 1) * lg 2 + (2^E - 1) * lg 2 = lg A + B$。

　　于是可以暴力枚举所有 M，算出 E 后再带回去检验误差。

　　此题的 EPS 选取有讲究，不能太大，可不能太小，10e-6 就差不多了，不然会 Wa。

代码如下

#include <bits/stdc++.h>
using namespace std;
 
#define INIT() ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define rFor(i,t,s) for (int i = (t); i >= (s); --i)
#define ForLL(i, s, t) for (LL i = LL(s); i <= LL(t); ++i)
#define rForLL(i, t, s) for (LL i = LL(t); i >= LL(s); --i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
#define rforeach(i,c) for (__typeof(c.rbegin()) i = c.rbegin(); i != c.rend(); ++i)
 
#define pr(x) cout << #x << " = " << x << "  "
#define prln(x) cout << #x << " = " << x << endl
 
#define LOWBIT(x) ((x)&(-x))
 
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
 
#define ms0(a) memset(a,0,sizeof(a))
#define msI(a) memset(a,inf,sizeof(a))
#define msM(a) memset(a,-1,sizeof(a))

#define MP make_pair
#define PB push_back
#define ft first
#define sd second
 
template<typename T1, typename T2>
istream &operator>>(istream &in, pair<T1, T2> &p) {
    in >> p.first >> p.second;
    return in;
}
 
template<typename T>
istream &operator>>(istream &in, vector<T> &v) {
    for (auto &x: v)
        in >> x;
    return in;
}
 
template<typename T1, typename T2>
ostream &operator<<(ostream &out, const std::pair<T1, T2> &p) {
    out << "[" << p.first << ", " << p.second << "]" << "
";
    return out;
}

inline int gc(){
    static const int BUF = 1e7;
    static char buf[BUF], *bg = buf + BUF, *ed = bg;
    
    if(bg == ed) fread(bg = buf, 1, BUF, stdin);
    return *bg++;
} 

inline int ri(){
    int x = 0, f = 1, c = gc();
    for(; c<48||c>57; f = c=='-'?-1:f, c=gc());
    for(; c>47&&c<58; x = x*10 + c - 48, c=gc());
    return x*f;
}
 
typedef long long LL;
typedef unsigned long long uLL;
typedef pair< double, double > PDD;
typedef pair< int, int > PII;
typedef pair< int, PII > PIPII;
typedef pair< string, int > PSI;
typedef pair< int, PSI > PIPSI;
typedef set< int > SI;
typedef set< PII > SPII;
typedef vector< int > VI;
typedef vector< VI > VVI;
typedef vector< PII > VPII;
typedef map< int, int > MII;
typedef map< int, PII > MIPII;
typedef map< PII, int > MPIII;
typedef map< string, int > MSI;
typedef multimap< int, int > MMII;
//typedef unordered_map< int, int > uMII;
typedef pair< LL, LL > PLL;
typedef vector< LL > VL;
typedef vector< VL > VVL;
typedef priority_queue< int > PQIMax;
typedef priority_queue< int, VI, greater< int > > PQIMin;
const double EPS = 1e-6;
const LL inf = 0x7fffffff;
const LL infLL = 0x7fffffffffffffffLL;
const LL mod = 1e9 + 7;
const int maxN = 1e4 + 7;
const LL ONE = 1;
const LL evenBits = 0xaaaaaaaaaaaaaaaa;
const LL oddBits = 0x5555555555555555;

int B, M, E;
double A;
string str;

int main(){
    //freopen("MyOutput.txt","w",stdout);
    //freopen("input.txt","r",stdin);
    INIT();
    while(getline(cin, str)) {
        if(str == "0e0") break;
        str[str.find('e')] = ' ';
        stringstream sin(str);
        sin >> A >> B;
        double v = log10(A) + B;
        
        For(x, 1, 10) {
            double tmp = log10(pow(2, x) - 1) - (x + 1) * log10(2);
            E = log2((v - tmp) / log10(2)) + EPS;
            if(fabs(v - tmp - pow(2, E) * log10(2)) < EPS) {
                M = x - 1;
                break;
            }
        }
        cout << M << " " << E << endl;
    }
    return 0;
}