前言
下午HHY还有AAK看到了这个
质问我Prufer序列是啥
被迫复习一波
引入
直接从题目看吧
[HNOI2004]树的计数
大概意思就是给你n个节点
告诉你每个节点的度数
然后问你根据这些度数能够生成多少棵树
看样例
4
2 1 2 1
画个图解释一下
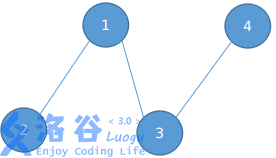

题目中给出的样例只有这两种情况,所以输出答案为2
我们更关心答案怎么来的,下面来讲一下(Prufer)序列
Prufer序列
性质一
- 存在无根树转为(Prufer)序列以及(Prufer)序列转为无根树两种操作,换言之,上述两者是互射的(可以互相转化)
证明一
-
无根树转(Prufer)
- 找到编号最小且度数为1的点
- 删除该节点,并且在序列中添加与该节点连接的节点
- 重复1、2操作,直至树上只剩下两个点
-
Prufer转无根树
- 设(Prufer)序列为集合(M),另一个集合 (G { 1,2,3…n })
- 每次提取M中最靠前的元素u与G中不存在与M且最靠前的元素v,将u与v连边,分别在两个集合中删除u、v。
- 最后将G中剩下的两个元素连边
举个栗子
看上面的第一个图

图转(Prufer)序列
先找到2,删除2和2->1连边,将1入列,删除1和1->3连边,3入列,序列就是“1,3”
(Prufer)序列转图
取出M中的1和G中的2连边,分别删除两个集合中的元素
取出M中的3和G中的1连边,然后……同上……
此时,M空了,G中只剩下了3,4,连接3,4就行了
性质二
(Prufer)序列是一种对有标号无根树的编码,长度为节点数-2
证明二
看证明一当中转换的要求
直至树上只剩下两个点
可以看到最后有两个点直接忽略
因为此时再判断顺序没有意义
那就是总数-2
性质三
对于给定的n个点度数,可以构造的树的数量为
$ (n-2)!/((d1-1)!×(d2-1)!×…×(dn-1)!) $
证明三
需要一丢丢前置知识
- 因为每个点的度数为d,在构造序列的时候
我们会发现,每有一个度数就会入序列一次
但是还要留一次给删除操作,就不入序列了
所以对于度数为(d_i)的点i
入序列的次数为(d_i-1) - 由性质一可知序列和图之间是一一对应关系
所以说n个点的序列长度为n-2
其全排列为((n-2)!) - 但是考虑到在序列中会有好多重复出现的点
比如1,1,2
按照位置全排列(A_3^3)有6种
但是实际上只有1,1,2 1,2,1 2,1,1一共3种
只需要(frac {A_3^3} {(d_1-1)!})就是正确的不重复的树的数量
于是乎,上述结论被证明
即
对于给定的n个点度数,可以构造的树的数量为
[(n-2)!/((d1-1)!×(d2-1)!×…×(dn-1)!)
]
代码实现
对于这个题目,需要判断几个地方
当转换prufer序列的时候,如果入列次数!=n-2,就一定有问题,输出0
还有,如果有的节点度数为0,那图就不联通,那就输出0
然后对于个数的求解
组合数打个表就可以了
Code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=155;
int c[maxn][maxn];
int ans,d[maxn];
int sum;
int n;
inline void pre(){
for(int i=0;i<=n;i++){
c[i][0]=1;
for(int j=1;j<=i;j++)
c[i][j]=c[i-1][j]+c[i-1][j-1];
}
}
int main(){
cin>>n;
if(n==1){
cin>>d[1];
if(d[1]==0) cout<<1<<endl;
else cout<<0<<endl;
return 0;
}
pre();
for(int i=1;i<=n;i++){
cin>>d[i];
if(!d[i]) return cout<<0<<endl,0;
d[i]--;
sum+=d[i];
}
if(sum!=n-2) return cout<<0<<endl,0;
sum=0,ans=1;
for(int i=1;i<=n;i++)
ans*=c[n-2-sum][d[i]],sum+=d[i];
cout<<ans<<endl;
return 0;
}
总结
没啥特别难得地方
就是性质三不太好理解
需要多找几个例子
讲真从去年到现在用的并不多
看过就当做是一个小知识拓展就好
蟹蟹~