由于学长暴力碾压
题解bolg拖更好几天
今天做个整理
水题大赛Ⅰ
这套题选两个题来说一说
C.SueJane的四叶草
题目描述
SueJane热衷于找寻四叶草,并坚信可以带来好运。
SueJane现在有株四叶草,她给这些四叶草按照好看的程度设定了排名。不存在两株四叶草的排名相同,因此,这个排名序列是一个1~n的排列。
SueJane现在想把这些四叶草按一定的位置排成一排。设排在第的位置的四叶草排名为pi,那么对于SueJane而言,如果对于1<=i<n,都能找到一个j,满足i<j<N且|pj-pi|=1(即i后面的位置有一株四叶草排名与i相差1),那么这个序列看起来就比较美观。比如一个1432序列是美观的,而2431就不美观(3后面不存在符合要求的数)。
此外,SueJane还对一些位置做出了限制,内容为规定某位置上的四叶草排名必须为。
现在她想知道,有多少个序列是满足条件的。请你求出满足条件的序列个数mod 998244353,不然就会被SueJane派去找四叶草。
输入格式
第一行为两个整数n,k,分别表示SueJane一共有株n四叶草,并且给出了k条限制。
接下来行,每行2个数x,y,表示第x个位置上的四叶草排名必须为y。
输出格式
一行一个整数表示答案。
样例输入
4 2
1 1
2 4
样例输出
2
solution
先讨论(k=0)的时候,总共的方案数是(2^{n-1})
手玩几个样例可以发现
考虑1~n-1个位置
因为从题意能看出来n是一个“万能”的位置
就是说任何一个不合法的没法处理的数字都可以放到第n位
考虑一个小的数列1234(不考虑第n位
- 2必须在1后面出现,因为1后面不可能有0
- 由于上面的限制,3必须在2后面,因为1在2前面,2后不可能有1
那么YY一下能感觉得到,1i必须按照1i排列
那么还剩下n-i-1位
我们还是按照顺序排好以满足条件
然后将两个数列插起来
因为互不影响所以可以直接插入
那么问题就变成维护两个这样满足条件的序列
定义f[i][j]表示第一个序列长度为i
第二个序列长度为j的答案
其中,满足条件i+j=n-1
现在再来考虑有限制的问题
若这个位置有限制
分三种情况
- 值为i,那么f[i][j]+=f[i][j-1]只能从j-1转移,因为i限制了他之前必须连续
- 值为n-j-1, 同上,f[i][j]+=f[i-1][j]
- 没有限制,就可以分别从i-1,j-1转移
处理完f数组
最后对最特殊的第n个位置进行判断
- 若a[n]有限制,那么就不管它,从前n-1个位置计算结果f[a[n] - 1][n - a[n]]
- 若a[n]没有限制,将f[i][n-i-1]累加即结果
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
#define int long long
using namespace std;
inline int read(){
int x = 0, w = 1;
char ch = getchar();
for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return x * w;
}
const int maxn = 5010;
const int mod = 998244353;
int f[maxn][maxn];
int a[maxn];
signed main(){
int n = read(), k = read();
if(!k){
int ans = 1;
for(int i = 1; i < n; i++)
ans *= 2, ans %= mod;
cout << ans << '
';
return 0;
}
for(int i = 1; i <= k; i++){
int u = read(), v = read();
a[u] = v;
}
f[0][0] = 1;
for(int i = 0; i <= n; i++)
for(int j = 0; j < n - i; j++){
if(!i && !j) continue;
if(a[i + j]){
if(a[i + j] == i) f[i][j] += f[i - 1][j];
if(a[i + j] == n - j + 1) f[i][j] += f[i][j - 1];
}
else{
if(i) f[i][j] += f[i - 1][j];
if(j) f[i][j] += f[i][j - 1];
}
f[i][j] %= mod;
}
if(a[n]) return cout << f[a[n] - 1][n - a[n]] << '
', 0;
else{
int ans = 0;
for(int i = 0; i < n; i++)
ans += f[i][n - i - 1], ans %= mod;
cout << ans << '
';
}
return 0;
}
水题大赛Ⅱ
[APIO2008]免费道路
题目描述
新亚(New Asia)王国有 N 个村庄,由 M 条道路连接。其中一些道路是鹅卵石路,而其它道路是水泥路。保持道路免费运行需要一大笔费用,并且看上去 王国不可能保持所有道路免费。为此亟待制定一个新的道路维护计划。
国王已决定保持尽可能少的道路免费,但是两个不同的村庄之间都应该一条且仅由一条 且仅由一条免费道路的路径连接。同时,虽然水泥路更适合现代交通的需 要,但国王也认为走在鹅卵石路上是一件有趣的事情。所以,国王决定保持刚好 K 条鹅卵石路免费。
举例来说,假定新亚王国的村庄和道路如图 3(a)所示。如果国王希望保持两 条鹅卵石路免费,那么可以如图 3(b)中那样保持道路(1, 2)、(2, 3)、(3, 4)和(3, 5) 免费。该方案满足了国王的要求,因为:(1)两个村庄之间都有一条由免费道 路组成的路径;(2)免费的道路已尽可能少;(3)方案中刚好有两条鹅卵石道路 (2, 3)和(3, 4)
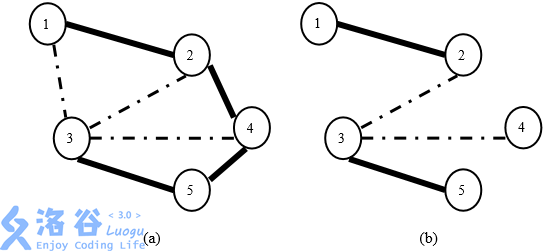
图 3: (a)新亚王国中村庄和道路的一个示例。实线标注的是水泥路,虚线标注 的是鹅卵石路。(b)一个保持两条鹅卵石路免费的维护方案。图中仅标出了免 费道路。
给定一个关于新亚王国村庄和道路的述以及国王决定保持免费的鹅卵石 道路数目,写一个程序确定是否存在一个道路维护计划以满足国王的要求,如果 存在则任意输出一个方案。
输入格式
输入第一行包含三个由空格隔开的整数:
N,村庄的数目(1≤N≤20,000);
M,道路的数目(1≤M≤100,000);
K,国王希望保持免费的鹅卵石道路数目(0≤K≤N - 1)。
此后 M 行述了新亚王国的道路,编号分别为 1 到 M。第(i+1)行述了第 i 条 道路的情况。用 3 个由空格隔开的整数述:
ui 和 vi,为第 i 条道路连接的两个村庄的编号,村庄编号为 1 到 N;
ci,表示第 i 条道路的类型。ci = 0 表示第 i 条道路是鹅卵石路,ci = 1 表 示第 i 条道路是水泥路。
输入数据保证一对村庄之间至多有一条道路连接
输出格式
如果满足国王要求的道路维护方案不存在,你的程序应该在输出第一行打印 no solution。 否则,你的程序应该输出一个符合要求的道路维护方案,也就是保持免费的 道路列表。按照输入中给定的那样输出免费的道路。如果有多种合法方案,你可以任意输出一种。
INPUT
5 7 2
1 3 0
4 5 1
3 2 0
5 3 1
4 3 0
1 2 1
4 2 1
OUTPUT
3 2 0
4 3 0
5 3 1
1 2 1
solution
一眼看过去感觉是个限制的Kruskal
想的是要把鹅卵石放前面先选
加一个计数器巴拉巴拉的判断
调试一个小时未果
然后看了T3T4未果
现在距离考试结束还有一个小时左右
就相当于两个不会,两个有思路没写出来
回过头看T1T2
硬把线段树切掉之后
继续想T2
调试太久了
就直接重构代码
写到kruskal函数的时候
忽然想到这个东西可能用不上
从反面想,只有三种情况是输出−1的
冰茶几就可以维护了
然后把必要的输出一下
剩下的随便选,把n−1补齐就够了
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
inline int read(){
int x = 0, w = 1;
char ch;
for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return x * w;
}
const int MAXN = 20200;
const int MAXM = 100100;
int n, m, k, fa[MAXN], tot, cnt;
struct edge {
int u, v, w;
} e[MAXM], ans[MAXM];
inline bool cmp1(edge e1, edge e2) { return e1.w > e2.w; }
inline bool cmp2(edge e1, edge e2) { return e1.w < e2.w; }
inline int find(int x) {
if (fa[x] == x) return x;
else return fa[x] = find(fa[x]);
}
inline bool link(int x, int y) {
x = find(x), y = find(y);
if(x == y) return false;
fa[x] = y;
return true;
}
inline void check(){
int tmp = find(1);
for (int i = 2; i <= n; i++) {
int ffa = find(i);
if (ffa != tmp) {
cout << "-1
";
exit(0);
}
tmp = ffa;
}
}
signed main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= m; i++) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
cnt = tot = 0;
for (int i = 1; i <= n; i++) fa[i] = i;
sort(e + 1, e + m + 1, cmp1);
for (int i = 1; i <= m; i++)
if (link(e[i].u, e[i].v) && e[i].w == 0)
tot++, e[i].w = -1;
if (tot > k) {
cout << "-1
";
return 0;
}
check();cnt = tot = 0;
for (int i = 1; i <= n; i++) fa[i] = i;
sort(e + 1, e + m + 1, cmp2);
for (int i = 1; i <= m; i++) {
int f1 = find(e[i].u), f2 = find(e[i].v);
if (f1 == f2)
continue;
if (e[i].w == 1 || tot < k) {
ans[++cnt] = e[i];
fa[f1] = f2;
if (e[i].w < 1)
tot++, e[i].w = 0;
}
}
if (tot < k) {
cout << "-1
";
return 0;
}
check();
for (int i = 1; i <= cnt; i++) {
if (ans[i].w == -1)
ans[i].w = 0;
printf("%d %d %d
", ans[i].u, ans[i].v, ans[i].w);
}
return 0;
}