下面来看一下很经典的“单链表逆序”问题。很多公司的面试题库中都有这道题,有的公司明确题目要求不能使用额外的节点存储空间,有的没有明确说明,但是如果面试者使用了额外的节点存储空间做中转,会得到一个比较低的分数。如何在不使用额外存储节点的情况下使一个单链表的所有节点逆序?我们先用迭代循环的思想来分析这个问题,链表的初始状态如图(1)所示:
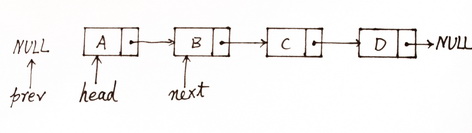
图(1)初始状态
初始状态,prev是NULL,head指向当前的头节点A,next指向A节点的下一个节点B。首先从A节点开始逆序,将A节点的next指针指向prev,因为prev的当前值是NULL,所以A节点就从链表中脱离出来了,然后移动head和next指针,使它们分别指向B节点和B的下一个节点C(因为当前的next已经指向B节点了,因此修改A节点的next指针不会导致链表丢失)。逆向节点A之后,链表的状态如图(2)所示:

图(2)经过第一次迭代后的状态
从图(1)的初始状态到图(2)状态共做了四个操作,这四个操作的伪代码如下:
head->next = prev;
prev = head;
head = next;
next = head->next;
这四行伪代码就是循环算法的迭代体了,现在用这个迭代体对图(2)的状态再进行一轮迭代,就得到了图(3)的状态:
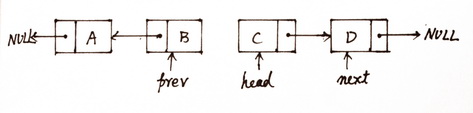
图(3)经过第二次迭代后的状态
那么循环终止条件呢?现在对图(3)的状态再迭代一次得到图(4)的状态:
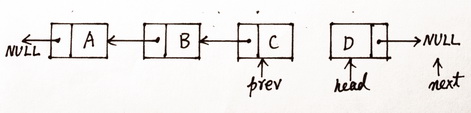
图(4)经过第三次迭代后的状态
此时可以看出,在图(4)的基础上再进行一次迭代就可以完成链表的逆序,因此循环迭代的终止条件就是当前的head指针是NULL。
现在来总结一下,循环的初始条件是:
prev = NULL;
循环迭代体是:
next = head->next;
head->next = prev;
prev = head;
head = next;
循环终止条件是:
head == NULL
根据以上分析结果,逆序单链表的循环算法如下所示:
|
61 LINK_NODE *ReverseLink(LINK_NODE *head) 62 { 63 LINK_NODE *next; 64 LINK_NODE *prev = NULL; 65 66 while(head != NULL) 67 { 68 next = head->next; 69 head->next = prev; 70 prev = head; 71 head = next; 72 } 73 74 return prev; 75 } |
现在,我们用递归的思想来分析这个问题。先假设有这样一个函数,可以将以head为头节点的单链表逆序,并返回新的头节点指针,应该是这个样子:
|
77 LINK_NODE *ReverseLink2(LINK_NODE *head) |
现在利用ReverseLink2()对问题进行求解,将链表分为当前表头节点和其余节点,递归的思想就是,先将当前的表头节点从链表中拆出来,然后对剩余的节点进行逆序,最后将当前的表头节点连接到新链表的尾部。第一次递归调用ReverseLink2(head->next)函数时的状态如图(5)所示:

图(5)第一次递归状态图
这里边的关键点是头节点head的下一个节点head->next将是逆序后的新链表的尾节点,也就是说,被摘除的头接点head需要被连接到head->next才能完成整个链表的逆序,递归算法的核心就是一下几行代码:
|
84 newHead = ReverseLink2(head->next); /*递归部分*/ 85 head->next->next = head; /*回朔部分*/ 86 head->next = NULL; |
现在顺着这个思路再进行一次递归,就得到第二次递归的状态图:
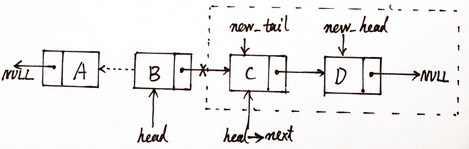
图(6)第二次递归状态图
再进行一次递归分析,就能清楚地看到递归终止条件了:
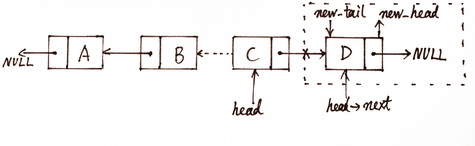
图(7)第三次递归状态图
递归终止条件就是链表只剩一个节点时直接返回这个节点的指针。可以看出这个算法的核心其实是在回朔部分,递归的目的是遍历到链表的尾节点,然后通过逐级回朔将节点的next指针翻转过来。递归算法的完整代码如下:
|
77 LINK_NODE *ReverseLink2(LINK_NODE *head) 78 { 79 LINK_NODE *newHead; 80 81 if((head == NULL) || (head->next == NULL)) 82 return head; 83 84 newHead = ReverseLink2(head->next); /*递归部分*/ 85 head->next->next = head; /*回朔部分*/ 86 head->next = NULL; 87 88 return newHead; 89 } |
循环还是递归?这是个问题。当面对一个问题的时候,不能一概认为哪种算法好,哪种不好,而是要根据问题的类型和规模作出选择。对于线性数据结构,比较适合用迭代循环方法,而对于树状数据结构,比如二叉树,递归方法则非常简洁优雅。